Appendix 1 An Embedded Viscous Cylinder in Pure Shear
The remote stress field shown in Figure 1 has principal stresses M+S and M-S, imagined as compressions. Eventually we shall want to consider the interface to be coherent and an overall compression M helps to make this plausible. But such an overall compression has no effect on the deformation or the associated stress variations; these can be fully discussed with remote principal stresses of S and –S, without the M. Additionally, for algebraic purposes it is convenient to have elongation rates as positive and hence to have tensile stresses as positive also; thus we consider a tension S to east and west and a compression –S from north and south. We use polar coordinates (r,q) with the interface at r = 1 and the direction of maximum tension as q = 0.
A solution of the corresponding elastic problem in absence of diffusion is given by Muskhelishvili (1963) and followed by Jaeger and Cook (1979), but their powerful general method is not readily extended to conditions that include diffusion. By contrast the following method is of narrow application but can be extended so as to shed light on diffusive behavior.
Assume that the stress field can be described by a series of terms of the form A.rN.cos mq; then for reasons of symmetry, m must be an even integer. Also, stress magnitudes must not become infinite at r = 0, so that inside the inclusion, no term can have N negative; similarly, stress magnitudes must not become infinite at remote points (![]() ) so that outside the inclusion, no term can have N positive.
) so that outside the inclusion, no term can have N positive.
To narrow the range of possibilities farther, it is convenient to look at a different term B.rn.cos mq and to name it f. The convenience lies in the fact that if we put
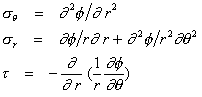 [1a,b,c]
[1a,b,c]
we automatically conserve momentum and describe steady flows, with no accelerations. Specifically for f = B.rn.cos mq,
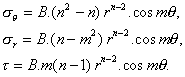 [2a,b,c]
[2a,b,c]
If the material remains continuous, it will also be true that
![]() [3]
[3]
where er and eq are linear strain rates and g is the engineering shear strain rate (twice the tensor shear strain rate). For a Newtonian material of viscosity N,
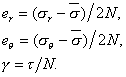 [4a,b,c]
[4a,b,c]
Let the direction of the cylindrical inclusion’s long axis be y. Then if ey = 0 (plane strain),
![]() [4d,e]
[4d,e]
If [2a,b,c] are used in [4c,d,e], the continuity equation [3] shows that
![]() [5a,b]
[5a,b]
In particular, for variation specifically with cos 2q, m = 2 and n = 4, 2, 0 or –2.
Because of the restrictions on the powers of r in the stress terms, N or n-2 as discussed above, we conclude that inside the inclusion n = 4 or 2 and outside the inclusion n = 2, 0 or –2. For the value n = 2, the r -dependence drops out of the stress terms; the pair m = 2, n = 2 describes just a homogeneous stress field such as would exist throughout the entire region if the inclusion were mechanically no different from the matrix.
The conclusion so far is that for the interior of the inclusion, a possible form is
![]() [6a]
[6a]
and for the exterior,
![]() [6 b]
[6 b]
where a, b, d, f and g are coefficients yet to be determined. At once, d is fixed by the stress state as r becomes infinite: at q = 0, sr(inf) = S so, from equation [2b], we need d = -S/2. The remaining coefficients a, b, f and g can be chosen according to whatever conditions we wish to satisfy at the interface.
The classical conditions at the interface are:
equal stresses, (sr)i = (sr)e and ti = te, [7a,b]
and equal velocities (to maintain coherence),
ui = ue radial and vi = ve tangential [7c,d].
These yield
![]() [8a,b,c,d]
[8a,b,c,d]
where R is the ratio (viscosity)i/(viscosity)e. Putting these expressions into (6a) and (6b) gives the same stress functions as are derived by Muskhelishvili (1963). In particular, the value a = 0 corresponds with the notable fact that the stress field throughout the inclusion is homogeneous, and this value of a is derived specifically from the interface conditions given. Any other interface conditions are likely to yield a non-zero value for a and an inhomogeneous stress field in the inclusion.
From the main text, we would like to find interface conditions that would allow for the material diffusing away from the north and south quadrants of the interface and accumulating at the east and west quadrants. To allow the radial velocities ui and ue to be unequal is an obvious choice; then at the east point, for example, a gap opens at the rate ue – ui and we can seek a balance between this rate and the rate at which material is arriving by diffusion. But once the process of deposition at the interface gets under way, it is not at all clear how the other interface conditions (7a, b and d) would change. For present purposes, we focus attention on just the moment when deposition begins, when the deposited film or sliver is infinitesimally thin, and propose that at this moment conditions (7a, b and d) can still be applied. This is clearly just a first step toward a more realistic analysis.
With ui and ue unequal, we can introduce b where ue = b.ui and now find:
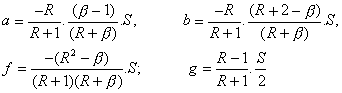 as before, [9a,b,c,d].
as before, [9a,b,c,d].
If we use these values to estimate ![]() and
and ![]() close to the interface and assume that the diffusivities of inclusion and matrix are also in the ratio R (Ke/Ki = R = Ni/Ne), we derive for any interface point:
close to the interface and assume that the diffusivities of inclusion and matrix are also in the ratio R (Ke/Ki = R = Ni/Ne), we derive for any interface point:
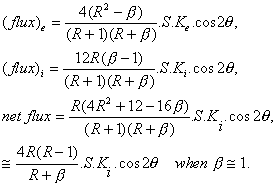 [10a,b,c,d]
[10a,b,c,d]
Also,
![]() [11]
[11]
so the diffusive fluxes take care of the excess or deficit at the interface if
![]() [12]
[12]
The product 4KiNi = L2 where L is a characteristic length of the material of the inclusion. Thus for example for R = 10, b = 5/4 if L = 1/6, or b = 2 if L = 1/3. Diffusion not only enables the matrix to deform more freely, it reduces the height of the stress maxima; for example, in the condition (R =10, L = 1/3 and b = 2), the radial compression at the north point is about 0.8 of its magnitude without diffusion.
For larger values of b or R, the exact form [10c] has to be used, and as R tends to infinity and ui tends to zero,
![]() [13]
[13]
For example, if L2 = 0.2, ue = S cos 2q/6Ne or specifically at the east point, ue = S/6Ne. (For comparison, if we replaced a rigid inclusion by material homogeneous with the matrix, then at the east point of a circle of radius 1 we should find ue = S/2Ne). Again, diffusion allows the matrix to deform as if the inclusion were much less viscous than it is. In fact algebraically, if we put L2 = 1 into equation (13), ue = S/2Ne as for a homogeneous material. But Appendix 2 shows that treating a material with microstructure as a continuum becomes increasingly unrealistic as L2 increases above 0.1 or 0.2; it is more the qualitative trend in these results that is of value.