Appendix 3 Anisotropic Gain or Loss
The whole of Appendix 1 rests on the observation that in the classical description of stresses around a cylindrical inclusion, ![]() If one’s assumptions about diffusion are:
If one’s assumptions about diffusion are:
![]()
conservation of volume, i.e.
![]()
linear strain rate e or dl/l.dt = (dV/V.dt)/3 in all directions,
(with elongations and tensile stresses positive) then whatever fluxes might be driven by gradients in the mean stress in the classical description, they would flow through the material without changing any dimensions, and would affect the stress field only by affecting conditions at the cylindrical interface. The purpose of this appendix is to explore the following alternative assumption: in place of
![]() for all directions, we postulate
for all directions, we postulate
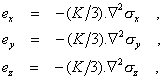 [1a,b,c]
[1a,b,c]
(which leave the volume strain rate ![]() as before). These, of course, are only the parts of the strain rate due to diffusion; if the material also creeps with viscosity N, the total effects are:
as before). These, of course, are only the parts of the strain rate due to diffusion; if the material also creeps with viscosity N, the total effects are:
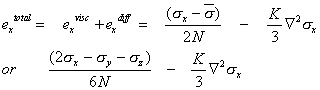 [2a,2b]
[2a,2b]
etc.
The intention is to pursue the ambition illustrated in Figure 5 using these alternative rheological assumptions.
[The postulates (1a, b, c) have been derived from fundamental concepts elsewhere, in a skeletal manner (Bayly 1988, 1996) and at greater length (Bayly 1992), and the associated flow law or constitutive relation is shown in Supplement 3. Here the ambition is not to advocate but merely to test the postulates by results: can they yield a stress field, a strain-rate field and a pattern of diffusive fluxes? If they can, do the results "look reasonable"?]
As in Appendix 1, we use polar coordinates, seek a stress function j rather than seeking the stresses themselves directly, and imagine a series of terms in j for any of which B.rn.cos mq can be taken as representative. As before, derived stresses are
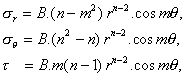 [3a,b,c]
[3a,b,c]
(conserving momentum), and again we wish to use the strain-rate relation that exists for any continuous velocity field,
![]() [4]
[4]
To use this relation, we need expressions for er, eq and g, for which we need in turn expressions for ![]() and
and ![]() and for the shear-strain consequences of the diffusion postulates in equation-set [1].
and for the shear-strain consequences of the diffusion postulates in equation-set [1].
For a single-valued scalar variable f, ![]() in polar coordinates is
in polar coordinates is
![]()
but sr is not a single-valued scalar: it is a scalar component of a tensor and thus a multivalued direction dependent scalar.
Then:
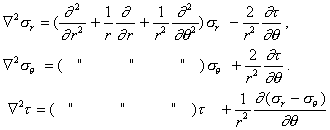 [5a,b,c]
[5a,b,c]
(see Supplement 1 below).For a term B.rn.cosmq in j these yield:
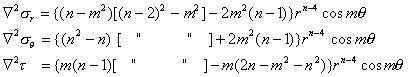 [6a,b,c]
[6a,b,c]
To use these relations, one can seek a suitable series of terms in j, as in Appendix 1 at equations [6a and b]. For any such series, stresses in the (r,q) plane can be derived using equations [1a-c] of Appendix 1. But in a material with self-diffusion, equations [4d and e] of Appendix 1 cannot be reached; the plane-strain condition no longer establishes sy = (sr+sq)/2; it yields only an equation like equation [2b] above, viz.:
![]() [7]
[7]
for plane strain. Hence one needs to seek not only a suitable series of terms for j but also a suitable separate series for sy, such that in combination with each other the results satisfy the geometrical relation [4] and the boundary conditions. Both series are likely to be infinite, and to find such a pair by analytical methods is a difficult task, not attempted here. Instead, for purposes of illustrating the problem, just two extra terms are added to j and two to sy. With these additions, the plane-strain condition is almost satisfied, and for geometrical continuity only a slight degree of material anisotropy is needed. Further comments on the usefulness and weaknesses follow the presentation of the results themselves. Even for this elementary approach, the problem was further simplified by taking the inclusion to be wholly rigid and non-diffusing; it is only the behavior outside the inclusion that we try to describe.