Supplement 3 Tensor expressions
To express the preceding ideas in a more comprehensive form, one needs to write the underlying constitutive relation thus:
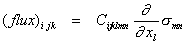
in which C could have 729 components (a sixth-rank tensor). But in an isotropic material, C has a non-zero component only when i= l, j=m and k=n, so the relation can be rewritten
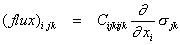 (no summation)
(no summation)
with 27 non-zero components in C. With conservation of volume,
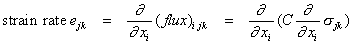
(summing over i) and if the material properties C are the same at every point,
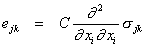
The two coefficients that were noted in the Discussion section can be used again; thus when j = k = i, C = J but when j = k![]() i, C = K as in equation [12]. The ideas in Supplement 2 suggest further that when j
i, C = K as in equation [12]. The ideas in Supplement 2 suggest further that when j ![]() k
k ![]() i, C = K again but that when either j or k = i (not both), C takes a third value designated H.
i, C = K again but that when either j or k = i (not both), C takes a third value designated H.
The viscous part of the strain rate is simpler:
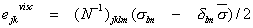
where N is of fourth rank. Again in simple materials, N has a non-zero component only when l = j and m = k. If one wished in a corresponding way to write:
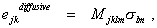
M would have 81 components, but only 9 non-zero, any one term being of the form
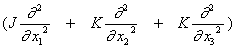
and the triplets being JKK
HHK
HKH
HHK
KJK
KHH
HKH
KHH
KKJ .
In this approach, M bears some resemblance to N but in fact remains fundamentally different because M is not formed purely from material properties, it contains the second-derivative operators.