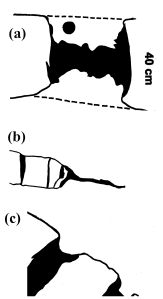
Filling of a Bouding Gap
Thus, two mechanisms contribute to filling the boudin gap. The rate of one is controlled by the rates of dissolution, diffusive transport, and re-precipitation, the other by the rheological behavior of the limestone and the geometry of the boudin gap. The observations indicate that the first mechanism is dominant when D/H << 1. At some critical value, D*/H, the two mechanisms contribute equally, and for higher values, the flow of softer rock into the gap dominates, although precipitation against the faces of the boudin may continue to result in the growth of pressure shadows. In examples like those shown in Figure 1, the area of reprecipitated calcite may be cast into the form of a boudin fill of uniform width D and height, H. Then, D is an upper bound on D*, the gap width at which both mechanisms contribute equally. From the examples in Figure 1, D may be estimated to lie between 3 cm and 12 cm. The smaller values are from measurements of gaps the further opening of which has been arrested; H is about 40 cm.
I derive quantitative models for each gap-filling mechanism. Their simultaneous operation is accounted for by the condition that the operative stress is the same. The bulk rate of extension for the mechanism involving dissolution, transport, and precipitation is
| [Dxx]ps = W[2/(W + H)](sxx szz)V0 | (1a) |
where
| W = [(6MV0/WH)K]/[(6MV0/WH) + K] | (1b) |
The diffusive transport coefficient (Robin, 1979) is
| M |
(1c) |
where D is the diffusivity in bulk fluid, x is the effective thickness of the diffusion path, c0 is the mean concentration of the dissolved component, R is the gas constant, T is the absolute temperature, and V0 is the specific volume of the solid phase. W is the length of the boudin, and W/H » 3 4. The mechanism is approximated as dissolution along the layer surfaces of the boudin, and diffusive transport along them and a crack between the boudin faces. Diffusion is driven by the gradient in chemical potential of CaCO3 along this path, m. Dissolution and precipitation are governed by a linear kinetics law of the form
| dD/dt = 2K(m meq) | (2) |
written here for precipitation onto the two surfaces of a single crack in the boudin gap, where meq is the equilibrating potential, the variation of which is dominated by the variation in normal stress (Kamb, 1961).
The parameter in (1b) has limiting values, corresponding to diffusion rate-controlling, K >> 6MV0/WH, or kinetics rate-controlling, 6MV0/WH >> K. As the absolute scale is reduced, a limit in which kinetics is rate-controlling is always reached, though this will probably not correspond to the natural example. At a large enough scale, diffusion is rate-controlling.
The model for flow into the boudin gap is that for the flow of a viscous fluid between two separating rigid plates (Jaeger, 1962). This approximation is good only if the width of the gap is much less than the layer thickness, or D/H << 1. It ignores the external flow that supplies the flux of material into the gap. For this mechanism
| [Dxx]f » (1/4h)(sxx szz)[2D3/H2W)] | (3) |
Equality of the two rates of extension at the same stress difference establishes an estimate of D*. The ratio of rates of extension for the two mechanisms is
| [Dxx]ps/[Dxx]f = [4hWV0/(W + H)](H2W/D3) = B(H2W/D3) |
(4) |
The ratio is the product of two dimensionless numbers, B, and a combination of structure dimensions that decreases markedly with boudin separation. Setting the ratio equal to unity
| D* = {B(H2W)}1/3 | (5) |
Diffusion is rate controlling here, so that
| D* = {24hMV02[H/(W + H)]}1/3 | (6) |
D
* does not depend on the absolute length scale. That means that D*/H decreases with absolute length scale.I informally call B the Bayly Number, in acknowledgement of Brian Baylys extensive contributions (e.g., Bayly, 1988, 1992,1996) to the investigation of the relative roles of diffusive transport and deformation in rock deformation. If B is small, little differentiation or segregation occurs. From (5), if B = 1, the transition gap width is of the order of the boudin thickness. However, the approximate models used would break down before such a gap is reached.
Among the parameters controlling the rates of the two mechanisms, the viscosity, h, and the effective diffusion path thickness, x, are probably the least well constrained. Using estimates for the parameters, excluding h and x, of D » 10-5 cm2/s, c0 = 3 x 10-5 gm/cm3, V0 = 0.368 cm3/gm = 36.8 cm3/mole, R = 8.3 x 107 erg deg-1 mol-1, T = 400K, and W/H = 3, I have evaluated D* for likely ranges in h and x. The result (Figure 2) accommodates not unreasonable values of these for the estimate D » D*.
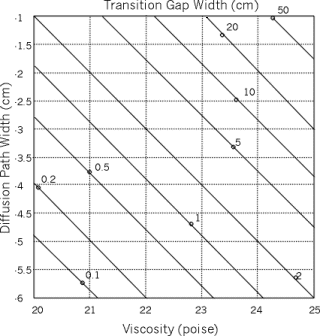 |
Figure 2. Estimates of transition boudin gap width D* as a function of choices of viscosity, h(poise), and effective diffusion path width, x (cm). See text for further discussion. |
Using these quantities, 6(Dx)(c0/RT)V0/WH » 1.25 x 10-21 x s/cm,
with x expressed in centimeters. The kinetic parameter for calcite at 100° C is the much larger quantity K = 10-16 s/cm. Hence, diffusion is rate-controlling.
From the computation, the required width of the diffusion pathway, x, is rather large for a plausible viscosity. For example, for h = 1021 Pa-s (1022 poise), x = 10-3 cm for D* = 3 cm. In computing the rate of dissipation in the system due to inflow of soft limestone, the dissipation associated with the flow towards the boudin gap is ignored. If this were included and were quantitatively important, contrary to our postulate, the estimates would be more in line with expectations.
The corresponding estimate of the Bayly Number is B = 1.15 x 10-22 x(cm)h(Pas). For x = 10-3 cm and h = 1021 Pa-s, this takes the small value B » 10-4. Hence, even small values of B may be associated with significant segregation. This is because of the large value of the geometric factor, H2W/D3, which goes to infinity as D approaches zero. At D = 3 cm, H2W/D3 = 6 x 103 for the present example.
The model may be used to estimate the variation in stress with gap width needed to open the boudin gap at a specified rate of deformation, or the proportion to which either mechanism contributes to the rate of opening as a function of gap width.