Interfacial Dissolution, Diffusion, And Precipitation In A Viscous Multilayer
The analysis follows the approach described in Johnson and Fletcher (1994). The multilayer is composed of layers of equal thickness, H, and viscosity h. The layers are separated by weak interfaces on which the slip rate, D{vs}, is set proportional to the resolved shear stress, sns, where s and n are local coordinates parallel and normal to the interface. Treating the interfaces as thin layers of thickness d* and viscosity h*,
D {vs}= (d*/h*)sns |
(16) |
The folding is vertically repetitive, with vertical axial planes, and occurs in shortening parallel to the mean orientation of the layers. Each interface is described by the locus, relative to the mean mid-plane of the layer,
| z = H/2 + Acos(lx) | (17) |
where l = 2p/L, and L is the fold wavelength.
A measure of the rate of differentiation is the rate of growth in the thickness of the "saddle reefs" into which, in the model, the phase transported from the fold limbs precipitates. This is just the difference in normal velocities, D{vn}, evaluated at a hinge. The rate of thickening of the layer, excluding the saddle reef, at the hinge is DxxH. The ratio -D{vn}/DxxH is a measure of the relative contributions of differentiation and layer deformation to the bulk rate of elongation along the hinge. From the analysis, I obtain
| -D{vn}/DxxH
@ {(4hV0/H)W/[1 + (4hV0/H)W]}[(2 + q*/2)/(k2/3 + q*)](lA)2cos(2lx) |
(18a) |
where
| W = K(MV0/l2)/[K + (MV0/l2)] | (18b) |
k = 2pH/L is a dimensionless wavenumber, and q* = (h*/h)(H/d*). Comparison with the result for the pressure shadow suggests the identification of the Bayly Number with the quantity
| B = (4hV0/H)W | (19) |
The expression (18a) thus also contains the factor [B/(1 + B)] times another dimensionless quantity containing q* and k, times the square of the maximum limb dip (in radians). As in the model for grain growth in a pressure shadow, the factor in B embodies the principle of "saturation," with reduction in the driving term as B increases. Thus, this factor varies between zero and unity as B ranges from zero to infinity.
Since differentiation only enters to second-order in the limb dip, lA, it cannot enter into the wavelength-selection process. The rate of amplification is
| dA/dt @ -DxxA - 2DxxA/(k2/6 + q*) | (20) |
In (20) and (18a), the exact result has been reduced to leading terms in k for k << 1, appropriate for large wavelength to layer thickness ratio, L/H >> 1. The approximations hold to terms ~ (lA)2, or up to limb-dips ![]() 10o - 20 o, above which both rates increase more slowly with limb-dip.
10o - 20 o, above which both rates increase more slowly with limb-dip.
Using (18a) and (20), I have determined the thickness of "saddle reefs", or the amount of differentiation, as a function of limb dip. Consider the limiting case q* = 0, in which layer interfaces are frictionless. Let t = t/t* be a dimensionless time, with t* = 1/[(12/k2)|Dxx|]. In the approximation that the basic-state shortening need not be accounted for, appropriate if fold amplification is rapid, or t* << 1/|Dxx|, (20) yields
l A(t) = lA(0)et |
(21) |
where A(0) is the initial amplitude. If n(t) is the thickness of the saddle reef at the hinge, from (18a), (19), and (21)
| d[n(t)/H]/dt = t*[D{vn}x = 0]/H = (½)[ B"/(1 +B")](lA)2 | (22) |
Integrating (22)
| n(t)/H = (Ό)[B"/(1 + B")](lA)2 | (23) |
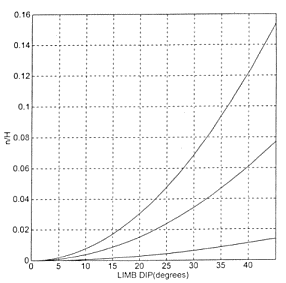
The thickness of the saddle reefs, or the amount of differentiation, is a function only of the Bayly Number and the limb dip. Consequently, B" can be estimated from field observations of n/H versus limb dip. The function (23) is plotted in Figure 3 for dips up to 45°
, probably beyond where it gives a good approximation, for small (B" = 0.1), intermediate (B" = 1), and infinite values of B". The limb dip at which the approximation breaks down is that dip at which the folds no longer appear sinusoidal.