If we consider a clast that is inclined at a small angle to S_se in which S_i is symmetrically crenulated, as the clast rotates towards S_2e one set of alternate limbs of the crenulations (Q domains) rotates towards horizontal and the other (M domains) rotates towards vertical (Fig. 8j). In terms of the pure shear component, S_i in the Q domains is rotating towards the shortening field whereas in the M domains it is in, or is rotating towards the extensional field. The domain boundaries lie in, and remain in the extensional field. The domains therefore have to increase in relative length. Three mechanisms are available for deformation within the domains - slip on S_i, homogeneous change in shape involving change in the shape of individual grains (intragranular mechanism), and fracturing. Of these mechanisms, under some conditions at least, slip is known to be a weak mechanism compared to the intragranular mechanism (Price and Torok, 1989; Williams and Vernon, in press). In the presence of a fluid, fracture, where there is extension perpendicular to S_i, is also likely to be a weak mechanism and at high strain rates is likely to be weaker than the intragranular mechanism.

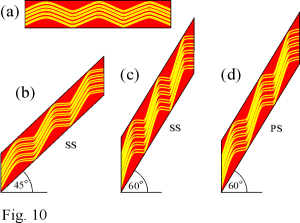
Figure 10 shows the same process in a folding situation where the strain is assumed to be homogeneous on the scale of a fold limb (analogous to one of the clasts). Here the domains as seen in profile, do not change in area and their relative widths are maintained. The crenulations become asymmetrical because in the Q domains the principal shortening direction is only slightly inclined to the crenulated surface whereas in the M domains it is more nearly perpendicular. Thus in the Q domains the folded surfaces shorten and move apart and in the M domains they lengthen and move closer together. This statement is true for a variety of initial interlimb angles. In this situation, in a strongly anisotropic material that is weak perpendicular to the folded surface and is weaker in tension than in compression (a general feature of rocks) there would be a natural tendency for slip to be the weak mechanism in the M domains and extensional fracturing to be the weak mechanism in the Q domains, leading to the situation modeled above. Once a reasonable fold is established it is not so important that the bulk strain path be noncoaxial as is demonstrated in Figure 10. In going from a limb dip of 45 to 60 the difference between a bulk simple shear parallel to the enveloping surface plus a rotation, and a bulk pure shear perpendicular to the axial plane of the fold is small (compare Fig. 10c & d,).

Fig. 10 Development of asymmetry in crenulations by enveloping-surface-parallel shear. (a) Initial shortening results in symmetrical crenulations. (b) Flexural slip is accompanied by spin of- and simple shear parallel to bedding. The crenulations become asymmetrical. (c) A further increment of simple shear and spin increases the limb dip to 60 , and further increases the asymmetry of the crenulations. (d) For comparison the dip is increased from 45 (as in b) to 60 (as in c) by pure shear shortening perpendicular to the axial plane (vertical). See text for further discussion.

In the M domains simple shear parallel to S_i would result in a decrease in the angle between S_i and the domain boundary and would increase the length of the domain thus satisfying bulk strain requirements. In the Q domain, slip on S_i accompanied by folding would be an adequate mechanism, but the initial width of the crenulation has already been determined by the wavelength for the foliated rock, and so still finer-scale folding might not be favoured. This is consistent with the fact that we do not see crenulations within the Q domains within the Woody Island rocks. This is generally true of differentiated crenulation. Another feasible mechanism in the Q domains would be opening of fractures parallel to S_i. This would accommodate the extension but would not produce a compensating shortening. However, if the process of slip on S_i in M domains and fracturing parallel to S_i in Q domains was accompanied by removal of quartz from the M domains and deposition of mica in the Q domains, a compensating shortening could be achieved at the scale of the combined M and Q domains. The mica stacks are readily explained as metamorphic mica growing epitaxially on detrital (or earlier S_i-parallel) micas (Hoeppener, 1956) that localised fracturing. Transfer of quartz and mica from M to Q domains would result in the prescribe strain. Removal of quartz from the system combined in some permutation with transfer or introduction of mica could be even better.

What actually drives the solution and deposition of quartz and mica remains a problem (see Fletcher, this volume). It is generally believed to be due to some mass transfer process either along a pressure gradient or from highly stressed to less stressed grain boundaries or simply due to flushing along channelways. Attempts to model the process using sophisticated numerical methods result in clogging of the channelways with quartz rather than removal of quartz (B.E. Hobbs, pers com. 1999). However, if it is assumed that the initial fabric is strong parallel to the crenulated foliation and weak perpendicular to it, the models predict a pressure difference between the two domains with high pressure coinciding with the M domains.

Another possibility is that shear in the M domains results in deformation of the quartz, at least near the surface (core and mantle style) and therefore in local high dislocation densities, whereas fracture, within mica grains, in the Q domains leaves the quartz grains essentially undamaged. The undeformed quartz might then grow at the expense of the deformed grains (e.g. Means, 1968; Meike and Wenk, 1988), or in a flushing situation, the deformed grains would tend to dissolve preferentially and be removed from the system.