Mark Jessell¹

This review discusses the attempts that have been made by geologists to numerically simulate the evolution of microstructures in rocks, and compares them with related research in the wider materials science community. In particular we focus on the application of techniques that have been used to predict texture development, grain boundary geometries, deformation in two-phase systems and crystal growth. The growth of this field in the near future promises to revolutionise our ability to predict and explain microstructure evolution in both geological and engineering materials.

Although the fundamental processes that control microstructure evolution in geological materials are the same as for engineering materials, there are some significant differences as well, namely the slow strain rates (10^-14 s^-1); the low crystal symmetry of most minerals; the poly-phase nature of most rocks and the complex chemistry of silicate systems. The long time scales involved preclude experiments that directly reproduce geological boundary conditions. In addition geologists are often involved with both the forward and inverse problems: how will a rock behave under given boundary conditions, but also what does a natural microstructure tell us about how a rock behaved when it was deformed 1 billion years ago?

The numerical simulation of microstructures in geological materials has progressed in parallel with techniques developed in the wider materials science community [1]. In recent years there has been an upsurge in interest in this field due to the easy access to powerful computers. Equally important has been the introduction of new measurement techniques such as Orientation Imaging Microscopy and Optical Orientation Imaging [2,3,4]. These techniques allow geo-scientists to systematically characterise the grain boundary topologies and textures of rocks with relative ease and in much more detail [5], thus provoking us to rethink what microstructural parameters we should use as indicators of specific processes.

In order to focus on outcomes, rather than just techniques, this overview is divided up into several sections, based on the principal microstructural characteristic that is being simulated.

The earliest simulation studies in geology were focused on predicting the texture patterns found in most naturally and experimentally deformed rocks. Lister and co-workers used a standard Taylor-Bishop-Hill formulation to study the development of textures in quartz and calcite rocks, Fig 1 [6,7,8,9,10,11]. Wenk and others have since extended this work to a broader range of minerals and to allow refinements of the TBH scheme such as the relaxed-constraints [12] and self-consistent approaches [13,14,15,16,17]. Their work was able to demonstrate that, even though many minerals do not fulfil the requirement for the strict application of the Taylor model, due to the limited number of slip systems available, many of the key features of natural textures could be accounted for.

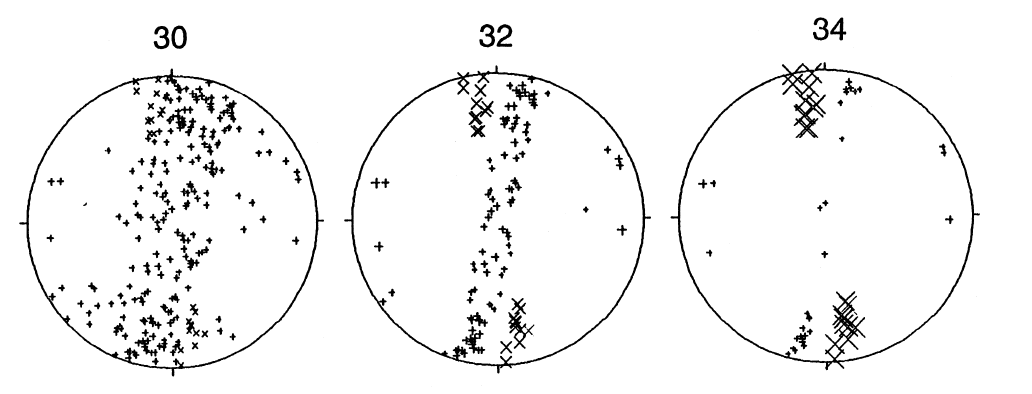
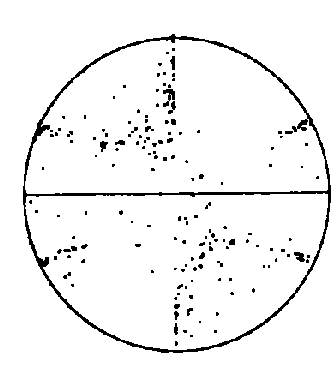
Figure 1. Simulation of c-axis texture development in model quartzites. a) Classical Taylor calculation for simple shear up to a shear strain of 3 [7]. b) Texture development caused by both intracrystalline slip and dynamic recrystallisation (i.e. nucleation and growth). Steps 30, 32 and 34 are shown, recrystallisation starts after step 30, the texture illustrated in step 34 does not change appreciably with further straining. Equal-area projection. The symbol + indicates old grains, ´ grains that have nucleated at least once; the size of the symbols is proportional to the grain volume [17].

An alternative approach recognises that in some minerals, such as trigonal symmetry quartz at low temperatures, only one slip system may be readily activated. Models that allow heterogeneous strain have been developed [18,19,20,21,22,23,24,25,26]. These models can reproduce the behaviour of, for example, ice and low temperature quartz. The question as to the role of grain boundary sliding in texture development has been investigated by allowing sliding interfaces between grains deforming with one slip system [27]. The model of Ribe [28] has been extended to simulate texture development in quartz when grain boundary sliding is the dominant deformation mechanism [29].

Under most conditions, rocks deforming by crystalline plasticity are also modifying their microstructure as a result of dynamic recrystallisation processes [30]. Jessell [31,32,33] drew upon experiments on cold worked copper [34] to support the assumption that the level of stored work is orientation dependent, and that the low crystal symmetry of the rock forming minerals would result in a larger anisotropy of stored work than is present in metals. He developed a hybrid scheme that combined the Taylor code of Lister with a Monte Carlo (MC) simulation that simulated the evolution of textures in quartz polycrystals by iterating between small increments of lattice rotations and grain boundary migration and sub-grain formation (Figure 2).

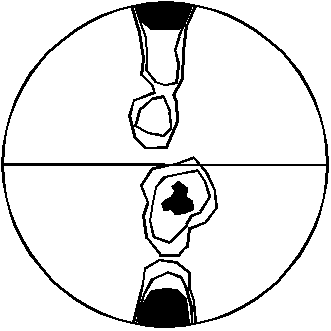
Figure 2. The simulation of microstructure development of quartz deformed in simple shear. The technique combines a Taylor analysis that predicts new lattice orientations and stored work, with a Potts model which uses the stored work term to drive grain boundary migration and sub-grain formation. a) Initial grain geometry, gray colours reflect c-axis orientations. Each complete grain is made up of 37 elements, and the entire model consists of 100x100 elements. b) Microstructure after a shear strain of 3. c) c-axis texture for simulation using the same critical resolved shear stress parameters as the model shown in Fig 1a. Contours are weighted to account for grain area [33].

The recrystallisation processes in these models were driven by a simple stored work term for each element in the MC simulation, as well as the more normal boundary energy derived neighbour relations [35]. These simulations show that a good correspondence with natural textures could be explained by the coupling of lattice rotations and dynamic recrystallisation. Comparable hybrid lattice rotation/recrystallisation schemes have recently been developed that replace the TBH scheme entirely with finite element codes capable of heterogeneous intra-crystalline deformation [36,37]. Another approach to modeling the effects on texture of dynamic recrystallisation in rocks has been to build in a grain size weighting to simulate the changes in grain size that may result from dynamic recrystallisation driven by orientation dependent stored work terms [17] (Figure 1b).

Finally a model has recently been developed that focuses on coupled rigid grain rotation and diffusive mass transfer [38] as a mechanism for predicting texture development.

There have been very few studies that have attempted to simulate the evolution of grain boundary geometries in rocks. Some of the works already mentioned did make some predictions about grain geometries, however the main focus of these two studies was the texture development [18,19,33]. Bons & Urai applied a modified version of the boundary dynamics model of Soares to grain growth [39,40]. This allowed them to study grain size and grain geometries for the case of normal grain growth in a system where homogeneous strain is combined with grain growth and demonstrate that the application of a bulk strain did not significantly alter the measured grain growth rates.

A hybrid simulation has recently been developed that consists of individual modules each of which represents a specific grain-scale deformation process, including a Finite Element (FE) description of deformation, a boundary dynamics model for grain boundary migration driven by surface and defect energy terms and grain boundary diffusion [41]. Microstructure evolution is achieved by the passing a data file (which describes the topology and geometry of the polycrystal) through each module in turn. This system has been applied to the problem of grain growth to investigate the role of surface energy anisotropy in modifying textures and grain boundary geometries [42]. Piazolo has applied this same simulation system to a systematic study of grain boundary geometries in deformed coarse and fine grain rocks [43]. These simulations have led to the proposal of new techniques to help identify deformation processes in naturally deformed rocks. Of particular importance with these hybrid techniques is the ability to make direct comparisons with the results of experiments on thin films directly imaged with optical microscopy (known as analogue experiments). Given the inaccessibility of geological systems to direct experimentation, these experiments provide the best constraints on our numerical simulations (Fig 3).

Figure 3. Comparison between a transmitted light microscopy thin-film grain growth experiment in a polycrystalline organic chemical (grey scale images) and a numerical experiment which used the same starting grain boundary geometry (white lines) [41].

As yet, there has been very little work on the development of microstructures during chemically driven nucleation and growth of new phases in rocks, and this area has enormous potential for further study [44].

While much of the work in geology has sensibly concentrated on single-phase systems, in reality most rocks consist of a mixture of two or more minerals. Several studies have looked at the specific case of a single rigid grain surrounded by a matrix of a weaker mineral. This case is important because it has been extensively used as an indicator of the kinematics and mechanics of deformation in natural settings. Apart from a number of analytical solutions, FE formulations have been used to study the flow field around the rigid object [45,46,47,48,49], the flow of the recrystallised (and mechanically weaker) rim of the rigid grain [50], and the pressure state around the rigid grain [51].

In terms of more general two-phase deformation, FE codes have been used to develop models predicting the flow properties of materials in terms of the end-member behaviour of its constituent components [52,53,54]. The work by Zhang and Piazolo also implicitly concerns poly-phase behaviour in the sense that each grain’s strength is orientation dependent [20,43].

Crystal growth at free surfaces plays a role in microstructure development in two main environments: during crystallisation from igneous melts, and during precipitation from fluids. An originally two-dimensional model has been developed into a three-dimensional simulation of crystallisation from a melt where an arbitrary number of seeds with different crystallographies may be specified [55].

The simulation of precipitation from a fluid into a dilating fracture is of particular importance in geology for two reasons: these mineralised fractures (known as veins) can contain economically significant ore minerals, and in addition the internal microstructures of these veins are used to estimate the kinematic history of their host rocks [56,57,58,59]. These simulations use a boundary dynamics approach to incrementally migrate the crystallisation front, both where this front is free to grow into an open space, and where the step-wise opening of the facing fracture surface controls the growth behaviour. This is thought to be particularly important in regions where periodic stress drops occur which related to earthquake cycles. When this happens during non-coaxial flow, the patterns of crystal development can be quite remarkable [60,61], and are beautifully reproduced by the equivalent simulations (Fig. 4).

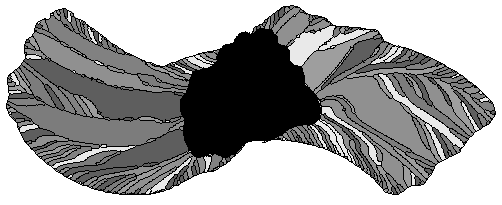
Figure 4. Fibrous crystal growth around a rigid mineral as it rotates clockwise during progressive simple shear. a) Example from Lourdes, France developed around a pyrite (FeS₂) grain. Width of image is 8mm. b) Numerical simulation of fibrous growth. Gray levels are proportional to orientation. [62]

The distribution of the publication dates in the references section of this review shows that the numerical simulation of microstructures is a blossoming field in the Earth sciences. Many of the techniques that have been applied have direct parallels in the materials science literature, however the complexity of natural geological systems has meant that in many studies the problems involve two-phase materials or multi-process behaviour. The solution of these problems will ultimately involve not simply the numerical simulation work, but an integrated approach that draws upon parallel transmitted light experiments where the observed temporal evolution of the microstructures can be used as constraints.

The author is indebted to the Australian Research Council for support of the Elle simulation code over the last 5 years. I would like to thank Lynn Evans and Janos Urai for their comments which greatly improved this manuscript. Finally I would like to thank T. Takeshita, H.-R. Wenk, G. Lister and D. Koehn for granting me permission to reproduce their figures.