(2) The description so far does not show any volume-element of material shrinking or expanding, --- losing or gaining material, --- by the diffusive mass transfer. The material that diffuses is deposited all in one location, at the interface, separate from the material it has diffused through. I would like to make the change illustrated in Figure 5, from the condition in part A to the condition in part B; that is, from the condition where deposition is strictly at the interface to a condition where deposition is distributed throughout a finite region of the host material.

The remainder of the text is an effort to circumvent these two defects.

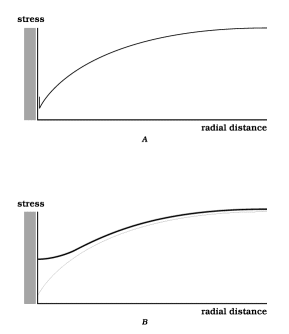Figure 5 Possible profiles of mean stress along the east valley. Part A shows a profile as discussed in the text and shown obliquely in Figure 2. It is in two parts, a portion that is concave downward along its full length and a vertical portion or step at the interface (represented by the short vertical line just outside the interface). These two parts meet in a point that can be regarded as a concave-upward portion with infinite curvature and infinitesimal width.By contrast in part B, the portion that is concave upward is of finite width. A stress field with this type of profile leads to material accumulating by diffusion in a dispersed manner throughout a finite region of the host material, rather than in the localized manner of part A. It is this type of profile that is sought in the second half of the text. For part B, one can still assume that the north profile has the form of the east profile inverted, and that exactly the same distribution of material is lost from north and south regions as is gained by the east and west regions; those aspects of the problem remain simple.