Diffusive Gain or Loss not Isotropic
  The present decade is interesting in that two different ideas about diffusive gain and loss are in use. Consider an extensive sample of material in which the stress is everywhere anisotropic and is also non-uniform. In particular consider a small spherical element somewhere within the sample: if the material is viscous but non-diffusing the element will undergo strain at constant volume, but if it is self-diffusing as well as viscous, it will deform with principal strain rates that in general do not conserve volume. In principle, one could run parallel experiments and, by subtraction, isolate just the strain rates attributable to the diffusive process. Then the two ideas are:

(1) these isolated or partial strain rates must be the same in all directions (i. e. diffusion by itself can turn a sphere only into a smaller or larger sphere)

or

(2) the partial strain rates form a set whose principal values at any point are in general different from one another (i. e. diffusion by itself could turn a sphere into an ellipsoid).

In the first theory, to predict diffusive effects one looks at magnitudes and gradients of just the mean stress; in the second theory, one has to look at all three separate principal-stress magnitudes rather than just their mean.

For illustration, consider the bending experiments in Figure 6. Everyone agrees that in cylindrical bending, diagram A, diffusion can be initiated with a flux from the inner surface to the outer. But in saddle bending, diagram B, opinion is divided. In the center of the slab, the mean stress is uniform from top to bottom, but vertical planes running north-south are compressed more strongly normal to the plane in the lower part of the test slab than in the upper part, while vertical planes running east-west are compressed more strongly in the upper part; that is, there are gradients in the normal-stress components on these planes, that cancel each other out to give no gradient in mean stress. One wonders, Do the gradients drive diffusive fluxes that contribute to the deformation of the saddle? As far as I know, no such experiment has been reported. To imagine spherical atoms like billiard balls favors the idea of no diffusion in such a slab, but to imagine dislocation loops, incomplete atom-planes and dislocation climb favors the idea that the gradients could drive some loops to shrink and some to swell. I wish to give both ideas serious attention and respect, but in this section it is the second that we explore.

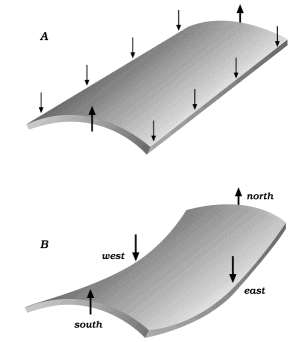Figure 6 Two possible bending experiments where diffusive transport in a vertical direction might occur.

[Idea 3: if the material itself is anisotropic, --- for example, having a microstructure that is flaky or fibrous --- loss by diffusion may be greater in one direction than in another for that reason. But this idea is wholly separate: in the present paper, the material itself has no anisotropy, it is from the stress state that the anisotropy of the strain rates arises.

For a fourth idea, concerning gain or loss at an interface, see Fletcher (this volume).]
 
Previous Section Home Next Section