The relevant equations are given in Appendix 3, and some of the results are shown in Figures 8 and 9. Figure 8 shows stress magnitudes along a radial line to the east in the direction-system of Figure 1. The effects of diffusion are greatest close to the interface. Again the effect is to diminish and smooth out peaks and extreme values; in particular the tangential compression s_q  no longer drops to such an extreme value. The change of curvature proposed in Figure 5 is seen: concave-upward curvature is noticeable in s_q  and perceptible in s_y  . By themselves, these upward curvatures would lead to accumulation of diffusing material and elongation in the tangential and y-directions. However, the theory assumes a totally coherent interface: the matrix is taken as firmly glued to the rigid inclusion and cannot elongate at the interface except radially outward. Instead of causing lateral swelling, then, the influx of diffusing material leads to a stress build-up e.g. from a to b in Figure 8; the material still swells, but constrictive stresses force the effect to occur by radial elongation.

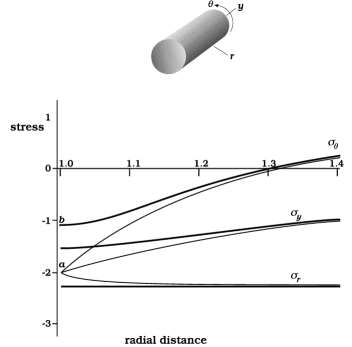Figure 8 Stress profiles along the east axis. Light lines are profiles unaffected by diffusion; in that condition, sy and the mean stress are equal so the curves here match Figure 7 (inverted) and Figures 5 and 2. Heavy lines show modified stress profiles such as might be present when diffusive transport occurs and gives unequal contributions to the strain rates radially and tangentially. In particular, the concave-upward part of the profile for sq   leads to accumulation of material and a tendency toward tangential elongation, but this is exactly countered by sq   now being greater than sy   and sr   which by itself would give tangential shortening. Compared with the light-line profiles, the change in magnitude of sq   and the change in curvature have to have equal and opposite effects on the tangential strain rate, if the matrix is to remain coherent with the inclusion.

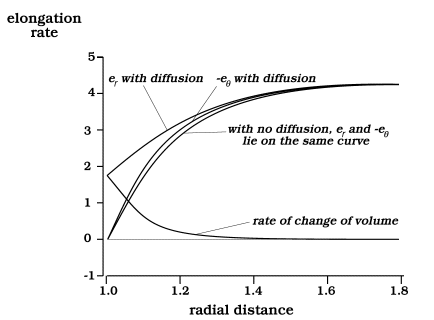Figure 9 Strain-rate profiles along the east axis. The matrix swells, gaining material by diffusion, but because of being coherent with the rigid inclusion, at the interface the swelling is entirely by radial elongation.

The strain-rate consequences are seen directly in Figure 9. The radial elongation e_r is noticeably larger when diffusion operates, whereas the tangential shortening hardly changes. Of course the latter is artificially pinned at zero at the interface by our assuming perfect coherence. With this constraint, it appears that as far out as 1.5 or 1.6 on the radial scale, the tangential shortening is actually a little greater when diffusion operates, as if the stress field over-compensates; but the equations are only a coarse approximate solution, and this detail in the curves for e_q   may be insignificant. The more important point is that we now see unequal strain rates in the radial and tangential directions, and increases of volume due to diffusion that are distributed through the matrix in a continuous manner rather than as a discrete sliver of new material at the interface.