|
The Broad Field |
|
Using reference directions as in Figure 2, consider a line from the inclusion’s center running north. As already shown, the profile of mean stress along such a line is as in Figure 7A. In absence of diffusion, if the inclusion is rigid, profiles of the north-south or radial stress and the east-west or tangential stress are as in Figure 7B (or if the inclusion is stiff but not rigid, see Figure 7C; here the separation distances p and q are in proportion with the materials’ viscosities). In all three diagrams, for the mean stress the diminution outward (to northward) is proportional to 1/r2 and, in the manner of Figure 2B, the upward curvature along this profile is exactly matched by a downward curvature of lines in and out of the page, --- the two curvatures balance. We now note that for the tangential stress, the upward curvature is clearly greater than for the mean stress and except right at the interface, the downward curvature is less; by contrast, for the radial stress, the upward curvature has been largely lost. Therefore, speaking geometrically, the tangential-stress surface has a net upward curvature and the radial-stress surface has a net downward curvature. If gradients on these surfaces separately drive diffusion, the tangential-stress variation will drive a net tangential accumulation outside the north part of the interface, and the radial-stress variation will drive a net radial loss; see Figure 7D. Along a line out to eastward, all the opposite effects occur, so that radial-stress variation drives a flux from north to east, whereas tangential-stress variation drives a flux from east to north. So far it remains true that no material element either swells or shrinks in volume, but in the north, there is radial shortening and tangential elongation while in the east, there is radial elongation and tangential shortening. It is reassuring to note that these are strains of the same type as are occurring simultaneously by viscous creep; anisotropic strain by diffusion adds to the deformation, it makes the material yield more readily; one sees greater strain rates and smaller stress peaks when this kind of diffusion is occurring than if diffusion were to act isotropically or not at all.
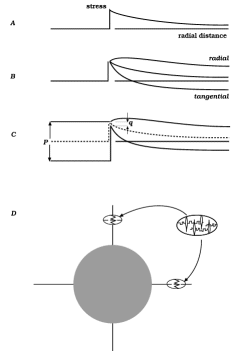 |
Figure 7 Stress profiles along the north axis and consequent gains and losses of material. |
(One might ask, about the north region for example: if, as above, radial-stress variation drives radial loss of material and tangential-stress variation drives tangential gain, would not most of the material that moves simply "slip round the corner" without ever leaving the site? No, radial loss and tangential gain at the same location go on at whatever rate the viscosity permits, given the stress difference at that location. We are looking here at additional radial loss that occurs because the radial compression is lower on either side of the north point, at neighboring points just to the east and west.)
|
| |
Previous Section Home Next Section |
