The basics of Darcian or advective flow through a permeable medium are described in Darcy’s equation for one-dimensional flow:

Q = - A · K · Df/Dx

(A.1)

This equation states that the flow rate, Q (m³ s^-1), along a line in the x-direction, is linearly proportional to the cross-sectional area, A (m²), through which the fluid flows, the hydraulic conductivity, K (m s^-1), and the gradient in hydraulic head, Df/Dx (m/m). A more general three-dimensional form of Darcy’s equation is:

q = - K · df/dx

(A.2)

where the vector q (m s^-1) is the rate of flow, per cross-sectional unit area, in the direction x.

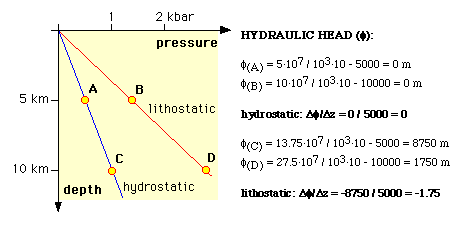
Hydraulic head is often confused with pressure when it is stated that "fluid flows from high to low pressure". Obviously, it is not so simple as water does not flow from the bottom of a glass (highest P) to the surface (lowest P). The hydraulic head (unit is metre) is given by:

f = P / rg + z

(A.3)

The first part of the equation is the pressure head, determined by the pressure, P (Pa), the fluid density, r (kg m^-3), and the gravitational acceleration constant, g (m s^-2). The second term, z (m), is the elevation head, which is simply the elevation above some datum level. If the pressure is simply the hydrostatic pressure, then the hydraulic head is the same at any level. If fluid pressure increase with depth is equal to the lithostatic pressure gradient (say 2.75·10⁴ Pa/m), then the hydraulic head gradient is 1.75 and fluid would flow upwards (Fig. A1). 
 

Figure A1. Graph showing lithostatic (red line) and hydrostatic (blue line) pressure-depth gradients in pressure-depth space, assuming specific densities of 2.7·103 kg/m3 for rock and 1.0·103 kg/m3 for water and a gravitational acceleration constant of 10 m/s2. Hydraulic heads are calculated for points A to D, showing that the hydraulic head gradient is 0 (no flow) for the hydrostatic pressure gradient and -1.75 for the lithostatic case, which results in upwards fluid flow.

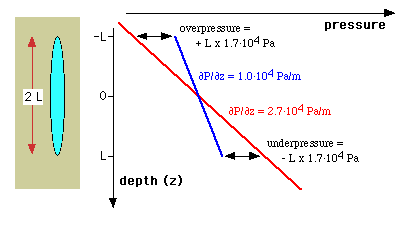
The hydraulic conductivity inside an open fluid reservoir is infinite and hence the hydraulic head inside a water-filled fracture is the same at any level in that fracture. As a consequence, the pressure inside such a fracture increases by about 10⁴ Pa/m with depth. Suppose now that we have a vertical fracture of length 2L that is filled with water (r~1·10³ kg/m³) in a surrounding rock with a density of 2.7·10³ kg/m³ (Fig. A2). It is clear that the vertical pressure gradient inside the fracture (1.0·10⁴ Pa/m) is different from the pressure gradient in the adjacent rock (2.7·10⁴ Pa/m). Suppose now that the pressures balance halfway the fracture, which level we take as a reference (z=0 m). At the upper tip of the fracture, the fluid pressure exceeds the rock pressure by L · 1.7·10⁴ Pa. The fluid is underpressured with respect to the rock pressure by the same amount at the bottom end of the fracture. This puts a limit on the length of an open fluid-filled fracture. Above some critical length, the overpressure at the upper end of the fracture causes the rock to further split open, while the underpressure causes the fracture to be closed at the bottom end. If the fluid volume is to remain constant, opening and closure must occur in tandem and when this happens the fracture moves upwards together with its fluid.
 

Figure A2. Pressure state inside a vertical fluid filled fracture, shown in a pressure-depth graph. The density difference between fluid (1.0·103 kg/m3) and rock (2.7·103 kg/m3) causes overpressure at the upper end of the fracture and underpressure at the lower end. Over- and underpressure are proportional to the length (2L) of the fracture.

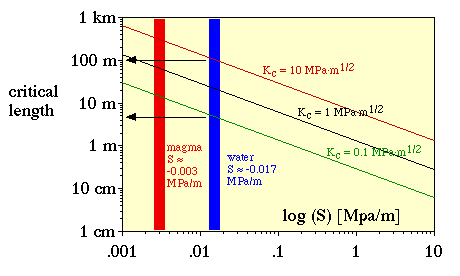
Secor & Pollard (1975) provided a simple equation to estimate the onset mobility of a vertical fracture:

Lmax = 1.36 · (Kc/S)2/3

(A.4)

L_max is the maximum length of a stable fracture, Kc is the fracture toughness and S is the effective normal stress gradient (S = dr / dz, ~ 0.015 MPa/m). The fracture toughness is about 1-3 Mpa·m^1/2 for intact crystalline rocks (granite, gneiss; Secor & Pollard 1975), but is probably lower for schists and low grade rocks, especially for fracturing parallel to schistosity. One should note that S is given here for a vertical fracture. The value of S is smaller for an inclined fracture, but can be significantly higher when a fracture is subject to a tectonic stress gradient, in which case S can possibly reach values of 0.1-1 MPa/m.

Figure A3 shows that vertical water filled fractures can reach lengths of about 5-100 m. Above that length, such fractures become unstable and rise rapidly, in the order of metres per second. A mobile fracture can thus easily ascend through the crust in a matter of hours. A mobile hydrofracture stops when the conditions of equation (A.4) are no longer satisfied. This can be because of rock type with a higher fracture toughness is encountered or when S decreases. The latter is probably the main reason for arrest. At any time it is easier for a fluid to enter pre-existing fractures than to propagate a fracture through intact rock. The presence of fractures thus causes the dispersal of fluid into these fractures, lowering S. For a hydrofracture to be mobile, the average pressure in the fluid must be lithostatic. Fluid is lost to the wall rock when a fracture reaches lower than lithostatic fluid pressures in the wall rock. Low fluid pressures and pre-existing fractures occur above the brittle-ductile transition and hence mobile hydrofractures are to be expected to get arrested at this level. 
 

Figure A3. Graph of critical vertical length as a function of effective normal stress gradient (S) (after Secor & Pollard 1975). For fracture toughnesses between 0.1 and 10 Mpa·m1/2, water-filled fractures are unstable due to their buoyancy above 5 to 100 m length. For comparison, granite magma-filled fractures become unstable when longer than 20 to 300 m. Tectonic stress gradients can give rise to much higher S-values