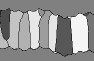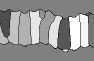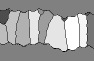Figure B1. Movie of grains growing by repeated crack-sealing. Growth is isotropic as envisaged in the model of Urai et al. (1991). Grains grow outward from the surface and thus converge on each other in embayments between ridges. Eventually, only grain boundaries are left that are growing vertically towards a ridge on the opposite side of the crack.

To further investigate the model of Urai et al. (1991), a computer program was written to simulate the crack-seal process. The model is only briefly described here, and the reader is referred to the full description of the model and a first systematic investigation with the model that are given by Bons (in press a) and Hilgers et al. (in press). In the 2-dimensional model, grains are defined by nodes that are linked by straight boundary segments. An initial horizontal surface fracture is created with a user-defined roughness. Every N time steps, the lower fracture surface is moved a user-defined distance and direction to simulate a crack-opening event. All grain surfaces that are then exposed to the open fracture grow outward by repeatedly moving the boundary segments over small distances one at a time. The segments are moved until they reach the other side of the fracture space (Fig. B2). The rate of growth is a function of the angle (a) between the boundary segment and the c-axis of a grain, which defines the lattice orientation. The type of function defines the growth habit of the crystal and therefore different "minerals" can be defined. In the examples below, two "minerals" were used:

• "Square mineral". The growth rate is fastest in the directions parallel and perpendicular to the c-axis. The habit of this mineral is that of a square.
• "Prismatic mineral". Growth is fastest parallel to the c-axis and slowest normal to it. A secondary growth rate minimum occurs at 30° to the c-axis, which gives the mineral a quartz-like prismatic habit.

Figure B2. Movie of crack-seal vein growth to illustrate the working of the program VEINGROWTH. Each crack-event, the lower wall rock is moved, in this case down and to the right. Exposed surface segments of grains grow into the crack. Their growth rate is determined by the relative orientation of the surface segment and the c-axis of the grain and the growth habit of the "mineral", in this case the prismatic "mineral". The orientation of the c-axes is shown by the shading: darkest for horizontal and white for vertical c-axes. The crystallographic control on growth rate leads to the development of faceted grain surfaces. However, if the crack is too thin, such facets may never fully develop before the crack is sealed again. In this example faceting is just forming before sealing.

Growth in an open cavity

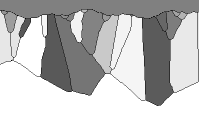
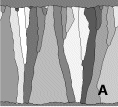
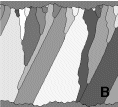
Growth in an open cavity best illustrates the effect of different mineral types on the morphology of the vein fill. Figure B3.a shows the result of 800 growth steps of the prismatic mineral into a wide open fracture with a rough surface. The shading of the grains is a function of the c-axis orientation. One can see that the grains with a vertical c-axis (light) quickly outgrow differently oriented grains. Figure B3.b shows the same for 640 growth steps for the square mineral. Both grains with vertical (light) as well as with horizontal (dark) c-axes are now the "winner" grains.
 

a  b

Figure B3. Movies of simulated vein growth into an open cavity. (a) Prismatic "mineral", growing for 800 time steps. Grains are elongate blocky in shape (no nucleation, except at beginning on wall rock) with faceted surfaces with the cavity. Growth is fastest in the direction of the c-axis and minerals with vertical c-axes (light) outgrow other grains (dark). (b) The same for the square "mineral". Growth is fastest parallel and normal to the c-axes and both grains with horizontal and vertical c-axes outgrow others.

Crack-sealing with a vertical opening trajectory - effect of crack-width

Three movies (Fig. B4) show the effect of the crack width. Figure B4.a shows growth in many (154), but small (2 pixels) vertical fracture opening events. Grain boundaries quickly get locked on ridges, resulting in little reduction in average grain width as growth progresses. The spacing of the ridges determines the width of grains. If, keeping all other parameters the same, the fracture opening is doubled to four pixels per event (Fig. B4.b), we see a decrease in locking capability of the ridges and a slightly larger average grain width developing. Increasing the fracture width to 16 pixels (Fig. B4.c) results in almost complete loss of locking capability of ridges. These simulations confirm the model of Urai et al. (1991), that the locking capability of ridges is a function of the width of the fracture relative to the roughness of the fracture. The rougher a fracture and/or the thinner the fracture, the better is the locking capability and hence the tracking capability of the vein crystals. The spacing between ridges determines the average crystal width when locking is strong.
 

a b c

Figure B4. Movies showing the effect of fracture width on the vein texture for the prismatic "mineral". All parameters are kept the same, except the vertical opening distance, which is (a) 2 pixels, (b) 4 pixels and (c) 16 pixels. See text for discussion.

Crack-sealing with an oblique opening trajectory - effect of crack roughness

Figure B5 shows three movies of growth with an oblique (Dx=-2 & Dy=4) opening direction, while all other parameters are kept the same except the roughness amplitude. The fracture surface is too smooth in Fig. B5.a for any ridges to lock grain boundaries. The average grain width increases in the growth direction and there is no tracking whatsoever of the oblique opening direction. Doubling the amplitude of the roughness (Fig. B5.b) leads to locking of some boundaries, but not all. Therefore, some boundaries follow the oblique opening trajectory, while others grow vertically. The result is a specific microstructure with some strongly elongate grains, some large blade like crystals and many "looser" grains (see Fig. 1.c in Bons & Jessell 1997). A further increase in surface roughness (Fig. B5.c) produces a better locking capability of the ridges and hence better tracking of the opening trajectory. 
 

Figure B5. Movies showing the effect of fracture roughness on the vein texture for the prismatic "mineral". Opening direction is 2 pixels to the left and 4 pixels down. All parameters are kept the same, except the fracture roughness, which varies from (a) smooth, (b) medium rough and (c) rough. See text for discussion.

Crack-sealing - change of opening direction

Finally, a case of growth with an abrupt change of opening direction is shown in Fig. B6. The case shown is for isotropic growth with a rough fracture surface, resulting in perfect tracking of the opening trajectory in the first growth period. After an abrupt change in opening direction, perfect tracking is maintained, but several fibres get truncated soon after the change in direction. Such a sudden increase in average fibre width is often seen associated with a change in opening direction (Fig. 14.b). The change in opening direction causes a change in the points where grain boundaries are locked. Temporary unlocking during the transition period frees the grain boundary for lateral movement and possibly the truncation of the grain.
 

Figure B6. Movie showing the effect of a change in opening direction for an isotropically growing vein material. Opening direction is 2 pixels to the right and 4 pixels down first and then 2 pixels to the left and 4 pixels down. See text for discussion.