Motivation For This Paper
1.1 The Issue
An ideal to which structural geologists aspire is to be able to infer the physical and chemical conditions of deformation and the constitutive behaviour of deformed rocks by examining the intricate geometry of the deformation. Thus, one would like to be able to say something about the temperature, the pressure, the strain distribution, the volume change distribution, the deformation rate tensor, the stress tensor, the fluid pressure, the fluid flux and rates of chemical reactions relative to the deformation rates and fluid flux rates by examining the geometry of the deformation. In addition, one would like to say if the material was behaving as a viscous material (perhaps even specify the power law exponent linking stress to deformation rate), or perhaps as elastoviscous or elastoplastic materials or as materials with even more complicated constitutive behaviour.
In this paper we select folding as an important and spectacular geological structure and explore recent progress towards the above ideal. Our emphasis is upon examining various (relatively simple) constitutive behaviours and exploring the fold geometries that arise from these behaviours. For simplicity, we restrict the discussion to only single layer folded systems.
The plan of this paper is as follows: In Section 1 we expand upon the issue involved here and point out that although simple theoretical rheological arguments predict single wavelength, strictly periodic fold trains, in reality in Nature we observe aperiodic or irregular fold geometries. We ask: Why is this so? In Section 2 we elaborate briefly on what we mean by the terms elasticity, viscosity and plasticity and introduce the concept of time scales for various deformation responses. In Section 3 we consider deformation of purely elastic or purely viscous single layer materials and follow in Section 4 with a consideration of elastoviscous materials where we show that two wavelength systems can occur. In Section 5 we consider folding of more exotic materials which couple elasticity and viscosity but with some form of non-linear behaviour also involved: fold systems with elements of fractal geometry and chaotic dynamics develop under such situations. Finally, we consider some recent developments involving the evolution of microstructures and microfabrics during folding or other deformations and the feedback such fabric evolution has on constitutive behaviour and hence upon full evolution. Section 6 summarises the paper.
The classical treatments of buckling of single layers embedded in another medium originated with Biot (1937, 1957, 1959, 1961, 1963, 1965), although identical developments were made by Ramberg (1963). These classical treatments are two dimensional, linear theories. The term linear means that only linear constitutive laws are examined (either elastic or linearly viscous but not power law viscous, plastic, or elastic-viscous behaviour); geometrical non-linearities related to large deflections or curvatures are excluded. The common result of all such treatments, no matter whether the layer or the embedding materials be elastic or linearly-viscous is that just one particular wavelength (the Biot dominant wavelength) is amplified with an exponential growth law. Thus, strictly periodic fold geometries always result from the classical theories no matter what initial geometry or initial deviations from the ideal planar state exist.
The problem is usually set up as shown in Figure 1.
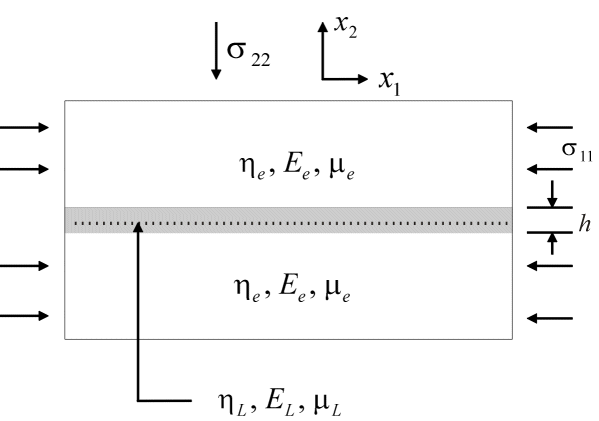
Figure 1: The problem to be considered in this paper. A single layer of thickness, h, and with Young’s Modulus, EL, elastic shear modulus, m
L, and viscosity,![]() L, is embedded in a medium with Young’s Modulus, Ee, elastic shear modulus,
L, is embedded in a medium with Young’s Modulus, Ee, elastic shear modulus,![]() e and viscosity,
e and viscosity,![]() e. The assembly is shortened in the
e. The assembly is shortened in the ![]() direction either by an imposed stress,
direction either by an imposed stress, ![]() , or by an imposed strain rate. The question is: What is the geometry of folds that form in the layer and how is this geometry influenced by the constitutive behaviour?
, or by an imposed strain rate. The question is: What is the geometry of folds that form in the layer and how is this geometry influenced by the constitutive behaviour?
A single thin layer of thickness, ![]() , is embedded in a medium and the whole assembly is subjected to either constant velocity or constant stress boundary conditions in the direction parallel to the initial orientation of the layer. Treagus (1973) has considered the situation where the shortening direction is oblique to the initial orientation of the layer. The constitutive parameters for the layer are the Young’s Modulus, EL, the elastic shear modulus, m
L, and the viscosity,
, is embedded in a medium and the whole assembly is subjected to either constant velocity or constant stress boundary conditions in the direction parallel to the initial orientation of the layer. Treagus (1973) has considered the situation where the shortening direction is oblique to the initial orientation of the layer. The constitutive parameters for the layer are the Young’s Modulus, EL, the elastic shear modulus, m
L, and the viscosity, ![]() L. Similarly, for the embedding medium these parameters are Ee,
L. Similarly, for the embedding medium these parameters are Ee,![]() e and
e and ![]() e respectively. The contrast in these parameters between layer and the embedding medium is known as the competency contrast (R), following Willis (1893) who proposed that competency was a measure of how well a material could support externally imposed stresses.
e respectively. The contrast in these parameters between layer and the embedding medium is known as the competency contrast (R), following Willis (1893) who proposed that competency was a measure of how well a material could support externally imposed stresses.
Relast is the competency contrast in the elastic parameters whilst Rvisc is the competency contrast in the viscosities. Notice that Relast can represent the contrast in either the Young’s Modulus or the shear modulus; these two contrasts are equal for a common Poisson’s Ratio for both the layer and the embedding medium.
As an example, for a linear viscous constitutive law, the Biot dominant wavelength is given by
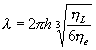 |
(1) |
And the growth coefficient corresponding to this wavelength for constant stress boundary conditions is
| (2) |
where s 11, s 22, are the stresses shown in Figure 1; see Mühlhaus et al. (1998).
However, natural folds are rarely, if ever, strictly periodic; that is they are rarely characterised by a single dominant wavelength. A clear example here is the ubiquitous existence in Nature of parasitic folds; here such geometries are characterised by two dominant wavelengths, a situation which is never predicted within the classical theories of Biot and Ramberg.
Moreover, even greater complexity in fold geometry is common, and some examples are shown in Figure 2. Strict periodicity with respect to wavelengths is very rare and we explore this complexity in a little more detail in an example below.



Figure 2: Examples of natural fold geometries. In (a) a thin planar laser beam is shown intersecting the surface of a folded layer. A series of such intersections is used to construct Figure 3.
Figure 3 shows a series of adjacent scans across the surface of a folded layer from the natural fold system shown in Figure 2(a). The scans were made using a thin planar laser beam and the resultant image, which represents the intersection of the planar beam with the folded surface, was captured using a video camera into a frame grabber.
Erratic behaviour in time series has been analysed for a variety of non-linear dynamic systems; here we are concerned with spatially erratic behaviour. Techniques for analysis of spatiotemporal chaos have been described by, for example, Mayer-Kress and Kaneko (1989) for coupled map lattices. We construct an "attractor" (see Figure 4) for the spatial pattern shown in Figure 3 in the same way that Packard et al. (1980, see also Takens, 1981, Crutchfield et al., 1986) obtained the attractor for a time series. We explore whether the evolution of one component of a system is determined by its interaction with other components, and reconstruct an ‘equivalent’ state space by examining the measured values at fixed space (rather than fixed time) delays with respect to a single component as though these space delays were new dimensions in this ‘equivalent’ state space. In this instance, the component of the system is the displacement of a given point on the profile of the fold relative to a datum. We are then able to examine the dimension (Figure 5) of this spatial attractor within different embedding dimensions, and infer the dimension of the system (for a succinct review, see Ruelle, 1990). The dimension of the system is representative of the number of degrees of freedom of the system, and therefore of the number of independent, non-linear differential equations required to describe the system.
Details of the procedure whereby Figure 4 is constructed may be found in Ord (1992). Again, following the procedures spelt out in Ord (1992), Figure 5 indicates that the "spatial attractor" shown in Figure 4 has a fractal dimension of 2.3. Thus, the attractor of Figure 4 is fractal; a periodic fold system would have given a plot with dimension exactly two.

Figure 3: A series of laser scans across the folded surface shown in Figure 2(a).
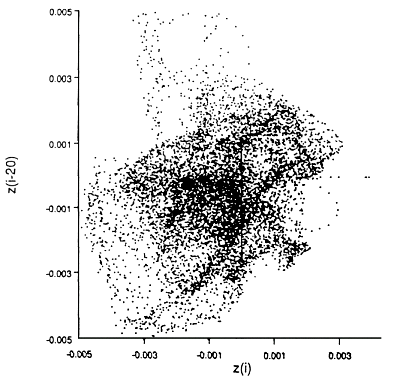
Figure 4: A "spatial attractor" for the series of profiles shown in Figure 3. See text for method of construction.
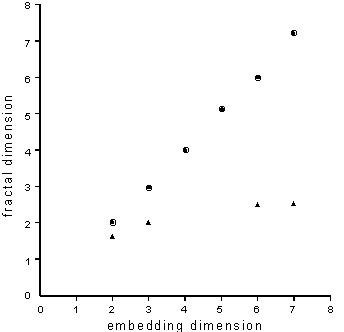
Figure 5: Plots of Fractal Dimension against Embedding Dimension for a random distribution (full circles) and for the "spatial attractor" shown in Figure 4 (triangles).
Even in these situations where an approximation to periodicity is developed, a question remains: Is the wavelength we observe in such situations really the Biot dominant wavelength, given for the linear viscous material as expression (1)? Or does mechanical behaviour more complicated than linearly elastic or viscous lead to wavelengths that differ from the Biot Wavelength?
For instance, many authors would propose that real geological materials behave as viscous materials with a non-linear, power law relationship between the magnitudes of strain rate and stress. The question therefore arises: Do these non-linear viscous materials also develop fold geometries in which the dominant wavelength is given by (1)? Of course, even asking this question raises the question of how we adequately define the viscosity for such a non-linear material. These issues are addressed in Section 3.
The aim of this paper is to explore the various issues and questions raised above. In part, the paper is a review of existing work although in the grand tradition of Win Means, to whom this paper is dedicated, the approach is to be didactic and to extract from the now diverse literature on the subject, those pertinent relationships and results that would enable us to go into the field and say something constructive about the rheology of the folded rocks we see from the geometry that is portrayed. Where necessary, we illustrate the conclusions made with new theory and computer simulations. We make no attempt to be comprehensive in our review.