The Problem
The observed non-periodicity of fold systems can have at least two explanations:
(i) Perhaps Biot-Ramberg type arguments concerning the amplification of a dominant wavelength need to be moderated by introducing a strong influence upon final fold geometry of initial geometrical or material imperfections. This is the argument proposed by Cobbold, 1975, 1977; Williams et al., 1978; Abbasi and Mancktelow, 1990, 1992; Mancktelow and Abbasi, 1992; Mancktelow, 1999. In particular, the results of Mancktelow, 1999, would suggest that at proposed geological strain rates of 10–14 s-1, initial geometrical irregularities always control the final fold geometry and Biot/Ramberg buckling processes play a relatively minor role.
(ii) Perhaps buckling behaviour is indeed the dominant behaviour but the controlling processes are more complicated than is proposed in the classical treatments of the problem. The basic tenet of such approaches is that non-linearities in the constitutive behaviour such as non-linear elasticity, coupling between elastic and viscous behaviour, strain- or strain rate softening or microstructural dependent yield or flow stresses lead to non-periodic geometries. We explore such developments in this area in Sections 4 and 5.
An important point to emphasize here is that if explanation (i) is important, then homogeneous deformation and the passive amplification of initial geometrical irregularities probably play a critical role in the development of folds we see in Nature. In extreme cases, the growth rate of dynamic folding is very low so that homogeneous deformation dominates all or much of the buckling histories and the end product of folding is essentially the passive amplification of the initial geometrical perturbations. During such folding processes, fold hinges are fixed at the inception of deformation and do not migrate along the layer with respect to material particles as the fold geometry evolves. An example of such a process is shown in Figure 6(b). Here the final geometry clearly represents the passive amplification of the initial irregular geometry of Figure 6(a). In other cases, the growth rate of dynamic folding may be able to dominate in later folding stages after significant initial homogeneous shortening, and hence folding can switch from the passive growth mode to the dynamic amplification mode. However, the limb dips of geometrical perturbations may have already reached finite amplitude fields (e.g. > 10° ) during the stages where homogeneous deformation and passive amplification dominate. Therefore dynamic folding in later stages of deformation may just follow the pattern of already amplified initial perturbations, so that again fold hinges do not migrate along the layer. These are the type of processes that are predicted by the classical Biot/Ramberg theories at very low competence contrasts (say R = 10 or below). One should emphasize that Mancktelow (1999) has reported this kind of behaviour for competency contrasts as large as 200 at strain rates of 10-14 s-1.
On the other hand, if Biot type buckling processes are relevant, then although there may be a period of initial homogeneous layer parallel shortening, a dominant wavelength will soon be selected and grow exponentially. As a result, a single wavelength, unrelated to the geometry of initial geometrical irregularities but determined by layer thickness and competency contrast, is developed ultimately.
An example is shown in Figure 6(c). The model starts from the same initial geometry (Figure 6(a)) as the previous example (Figure 6(b)) but in contrast a regular fold train with a dominant wavelength is ultimately developed; note that the change in folding is purely due to the change in strain rate, the effect of which on folding will be discussed subsequently. Here there must be some migration of fold hinges along the layer relative to the positions of material particles but such migration only occurs during early folding stages while limb dips are still low. Notice that the positions of initial irregularities here play no part in controlling the positions of fold hinges (Figure 6(c)). Again, one should emphasize that Zhang et al. (1996) have reported such behavior for competency contrasts as low as 20 so there is a problem in reconciling the results of Zhang et al. (1996) with those of Mancktelow (1999). This issue has been explored in Zhang et al. (2000).
We discuss these problems in subsequent sections but foreshadow the solution here.
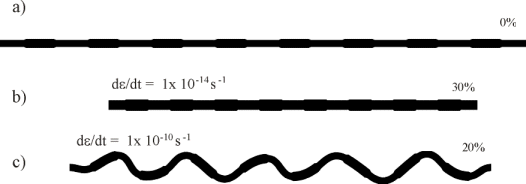
Figure 6: Folding of a layer, with initial rectangular geometrical perturbations, at two different strain rates. a) Initial geometry of the layer. b) Final layer geometry of the model with a strain rate (d
e/dt) of 1x10-14 s-1 at 30% bulk shortening; domination of homogeneous straining plus some passive amplification of initial perturbations. c) Final layer geometry of the model with a strain rate (de/dt) of 1x10-10 s-1 at 20% bulk shortening; domination of dynamic folding. The competency contrast (R) is 50 in both models. Corresponding material properties are: hL = 5x1020 Pa s, he = 1x1019 Pa s, EL = 1.75x1011 Pa, Ee = 3.5x109 Pa, mL = 7x1010 Pa and me = 1.4x109 Pa.In the classical Biot/Ramberg types of analyses the growth of a fold arising from a buckling instability follows a law of the type
  |
(3) |
where w is the displacement of the layer,
is a constant, 
is the growth coefficient and t is time. In general, 
is a function of stress in the layer and of competency and of competency contrasts; see for example, expression (2).
For materials which display viscosity there is also a viscous relaxation of stress once a given strain is attained.
Both the processes of viscous amplification and of viscous relaxation can be characterised by time constants which are (i) the time, w-1, for the amplitude to grow to e times the current value (where e is the base of the natural logarithms), in the case of fold amplification by buckling, or (ii) the time for the stress to decay to 
of its current value in the case of viscous relaxation.
Clearly, if the time constant for buckling amplification exceeds that for viscous relaxation, the buckling instability will grow by dynamic amplification. On the other hand, if the time constant for buckling amplification is much less than that for viscous relaxation then dynamic buckling will be very weak and the result is the domination of homogeneous deformation. We show in Section 4 that the former corresponds to the results of Zhang et al. (1996) whilst the latter corresponds to the results of some of Mancktelow’s models (1999).