3.2.1. The crack-seal mechanism

Before discussing the processes and causes for precipitation inside a vein, it is worthwhile to briefly discuss the crack-seal mechanism. The crack-seal mechanism was first introduced by Ramsay (1980) and has quickly become the accepted mechanism for the formation of fibrous/elongate blocky veins (Cox et al. 1986, Urai et al. 1991, Kirschner et al. 1993). The mechanism itself does not dictate any fluid or solute transport mechanism, nor a specific cause for precipitation inside a vein. The essence of the crack-seal mechanism is the repeated formation of a crack which is subsequently sealed by precipitation of vein forming material inside that crack. The crack-seal cycle can be repeated hundreds of times, typically adding about 10 µm to a vein each cycle (Fisher & Brantley 1992). The crack-seal mechanism can explain many parallel wall rock inclusion trails that are often found in veins (Fig. 13 & 21). The effect of the crack-seal mechanism on the morphology of vein forming crystals (stretched / elongate blocky / fibrous) and the tracking-capability of elongate crystals is further discussed in Appendix B.

3.2.2. Vein growth without fracturing

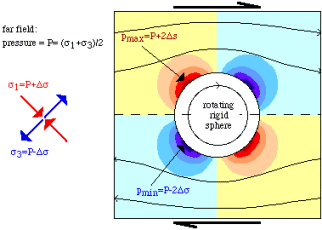
Probably the most clear-cut case of vein growth without fluid flow, but by diffusional solute transport is a pressure fringe adjacent to a rigid object (e.g. a pyrite grain). The presence of a rigid object in a deforming/stressed rock causes a perturbation of the stress and pressure field around the object (Durney & Ramsay 1973, Strömgård 1973, Durney 1976, Selkman 1983). The sides of the object facing the highest compressive normal stress experience the highest pressure, while the sides facing the lowest normal stress experience a relative low pressure (Fig. 24). This pressure difference can drive dissolution at the high pressure sides, diffusional transport to the low pressure sides and precipitation there to form the pressure fringes. This process can occur without the formation of a (thin) crack at the low pressure sides of the rigid object. Pressure fringes are usually fibrous and generally have no wall rock inclusions and therefore show no typical indicators for repeated crack-sealing. However, crack-sealing can occur, as has been shown by Lister et al. (1986) for biotite porphyroblasts where radiator structures formed in pressure shadows. 
 

Figure 24. Flow lines (arrow lines) and pressure contours around a spherical object in a homogeneous linear viscous matrix deforming in horizontal dextral simple shear. Far away from the object the principle stresses are at 45° to the flow plane. If the far field pressure is P, then s1=P+Ds and s3=P-Ds and the differential stress is 2Ds. The maximum stress perturbations occur on the surface of the rotating sphere, where stresses range from P-2Ds (blue) to P+2Ds (red). The difference in pressure can drive diffusional material transport from the red quadrants to the blue ones, where precipitation leads to the growth of pressure shadows (distributed precipitation) or pressure fringes (localised precipitation). The flow field and pressure contours were calculated with equations from (Chwang & Wu 1975), modified for simple shear.

It may be important that pressure fringes are usually fibrous (not elongate blocky) and appear to form without any brittle failure: there are no microstructural indicators for fracturing and the stress and pressure field around the object provide the driving force for material transport and precipitation in the fringe. This supports the hypothesis that the fibrous crystal morphology may form in the absence of fracturing, as was also proposed by Taber (1918) and Mügge (1928), and more recently by Durney & Ramsay (1973), Janssen & Bons (1996) and Bons & Jessell (1997). In the absence of fractures, diffusion is the only viable transport mechanism and we may infer that fibrous veins are indicative of diffusional material transport. 

Taber (1918) argued that the base of fibrous crystals must be in contact with a supersaturated solution in pores in the wall rock. Fibres "grow out of" the pores, which means accretion of new material is at the wall rock - vein interface. The work of Taber has recently been replicated by Means and Li (1995a,b) and Li and Means (1995), who produced very natural looking fibrous textures, without any fracturing. Mügge (1928) argued that the absence of growth competition in fibrous aggregates indicates the absence of an open fracture in which the crystals grew. He delineated three cases:

(1) The opening rate of the vein (fracture) is faster than the maximum potential growth rate (on fastest growing crystal faces). Euhedral crusts of crystals form.

(2) The opening rate of the vein (fracture) is slower than the maximum, but faster than the minimum potential growth rate of crystals. Growth is partly constrained and elongate-blocky crystals would form with a crystallographic preferred orientation (CPO).

(3) The opening rate of the vein (fracture) is slower than the minimum potential growth rate. The surfaces of the growing crystals remain in contact with the opposite wall rock at all times and growth competition is therefore inhibited. Fibrous crystals form without the development of a CPO.

Pabst (1931) measured c-axes orientations in fibrous pressure shadows to test the hypothesis of Mügge (1928) and indeed found that the fibres did not develop any CPO. The stretched and elongate-blocky quartz veins of Cox (1987), on the other hand, did show a CPO, which is in line with Mügge’s (1928) hypothesis that such veins fall into category (2), with the refinement by Ramsay (1980) that opening rates are not constant, but that space is created in distinct steps by repeated crack-events. 

In the case of fibrous growth in pressure fringes, the driving forces for diffusional transport and precipitation are evident: the stress and pressure perturbation caused by the relatively rigid object. Can growth without fracturing in other fibrous vein types be explained, when the transport mechanism and cause for precipitation is less evident? Well developed antitaxial fibrous calcite veins in shales are found in Opaminda Creek (northern Flinders Ranges, South Australia). The Young’s modulus of calcite is at least about double that of shale (Birch 1966). An isolated (lenticular) calcite vein therefore forms a hard object relative to the surrounding shale and, during deformation, would (as for rigid pyrite grains) develop a pressure gradient around itself (Fig. 25), which can drive further growth of the vein. Such veins can then be regarded as ‘self-supporting’ pressure fringes. Propagation at the vein tips, where a strongly localised stress perturbation occurs, lengthens the vein as it widens, which probably enhances the process. 
 

Figure 25. Pressure contours for deformation of a lenticular inclusion in a linear viscous matrix. The model is shown on the left with the imposed vertical shortening boundary conditions (arrows). Contours for pressure are shown on the right for the whole model (yellow square) and for the area around the inclusion tip (orange square). (a) Pressure contours for deformation around a hard inclusion (viscosity 100 x that of matrix). Pressure inside the hard lens is high, but the highest pressure is found at the inclusion tips. Lowest pressure is found at the sides of the inclusion. (b) Pressure contours for a soft inclusion (viscosity 0.01 x that of matrix), simulating an open fracture. Lowest pressure occurs inside the inclusion and highest pressures at the sides of the inclusion. Except for the singularity at the tip of the hard inclusion, the solutions for hard and soft inclusion are the inverse of each other. (c) Pressure profile along paths A-B and A-C for a hard inclusion. Any transport down the pressure gradient would bring material from the inclusion tip area (C), but also from the far field (B) to the surface of the inclusion. This could explain the growth of antitaxial veins without fracturing. (d) Pressure profile along profile A-B for a soft inclusion or fracture. The highest pressure occurs adjacent to the fracture, which would be the site of maximum dissolution if dissolution-precipitation creep operates. Material transport could be towards the vein, but possibly also away from the vein, down the pressure gradient. Pressures were calculated with the finite-element package BASIL (Barr & Houseman 1992, Bons et al. 1997).

For this process to work, a ’seed’ vein must already be present. Many of the antitaxial fibrous veins at Opaminda Creek have a median zone that is actually blocky in texture and fibrous crystals started growing from the surface of this zone (Fig. 19). The veins may have thus started their life by another process than described above and subsequently grew wider and longer by material transfer and precipitation by a self-supported pressure gradient. It should also be noted that fibrous veins at Opaminda Creek occur as isolated lenses, but also as long (metres) and thin (cm’s) fracture-shaped veins, both of which are antitaxial and fibrous. The shape of these veins is probably related to fracturing, which may have only seeded these veins. However, the actual driving force for subsequent fibrous growth in fracture-shaped veins is not known.

3.2.3. Vein growth in fractures

Fractures are the most common sites for veins to form, as fractures provide space for precipitation and preferred pathways for fluids to flow through. Two main causes for precipitation inside fractures can be distinguished:

a) Vein-forming material is derived from a fluid that resides in both fractures and surrounding wall rock. The conditions inside the fracture and in the wall rock are different, such that a fluid that does not produce any (significant) precipitation in the wall rock does precipitate one or more minerals inside the fracture. Vein formation can then occur in the fracture by either diffusional transport in a possibly stagnant fluid or by flow of a fluid that brings local fluid from the wall rock into a vein. Again we can distinguish two cases:

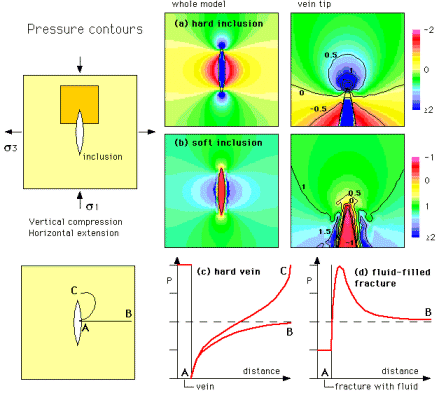
Minerals precipitating in a fluid filled fracture grow into an open fluid, even though there may only be a few microns of free space, before the other side of the fracture is encountered. The shape of the crystals is then determined by the growth competition of different minerals and the competition between crystals with different crystallographic orientations. The resulting texture in the vein depends on several factors (Urai et al. 1991):

- the morphology of the fracture surface (smooth, rough);

- the width of the fracture;

- the growth habit of the vein forming mineral(s).

The effects of the different factors are discussed and illustrated in more detail in Appendix B. Microscopic morphologies that result from crack-sealing are typically elongate blocky and stretched crystals. The first form when repeated fracturing occurs on the same fracture surface, while the second is the result of repeated fracturing along different surfaces.

3.2.4. Coupled fracturing and fluid flow

High fluid pressure, close to lithostatic, can only form in a low permeability regime which prevents rapid drainage of the overpressured fluid (Sibson et al. 1975, Nur & Walder 1992). Close-to-lithostatic fluid pressures therefore are generally found only at deeper levels in the crust, roughly below the brittle upper crust. As mentioned above, high fluid pressure can create high permeability through fracturing - especially when helped by deformation (Cosgrove 1993). The ensuing high permeability allows draining of fluid, which brings the fluid pressure down towards hydrostatic levels. Closure of dilatant fractures and sealing of fractures by precipitate reduces permeability and fluid pressures eventually rise again. This cyclical behaviour of rising fluid pressure until sudden fracturing, release of fluid ("burping") and reduction of fluid pressure is known as "fault valve behaviour" or "seismic pumping" (Sibson et al. 1975, Nur & Walder 1992, Thompson 1997, O'Hara & Haak 1992) (Fig. 28). It is generally used to explain extensive veining, such as the gold-bearing quartz veins in mesothermal gold deposits (e.g. Victorian and Yilgarn gold fields in Australia (Cox et al. 1986, Sibson & Scott 1998)).
 

Figure 28. Movie illustrating the effect of an increase in fluid pressure (dial on right), which brings the Mohr-circle to the point of tensile failure. Drainage of the fluid through the newly created fracture, causes a decrease in fluid pressure again, bringing the situation back to the start of the cycle.

Changes in temperature (Eisenlohr et al. 1989) and pressure (Vrolijk 1987, Henderson & McCaig 1996) are the primary causes for precipitation of vein forming material from a fluid that is flowing through fractures. Chemical interaction with the wall rock and mixing of different fluids are other possible causes (Boullier et al. 1994), but as veins occur in almost any type of rock, these can not be the main reason for precipitation. As quartz is the main mineral in large fracture hosted vein sets, the discussion below focuses on the solubility of silica. Silica solubility is primarily dependent on temperature (Fig. 29), except at high temperature and low pressure, where the solubility becomes strongly pressure-dependent. 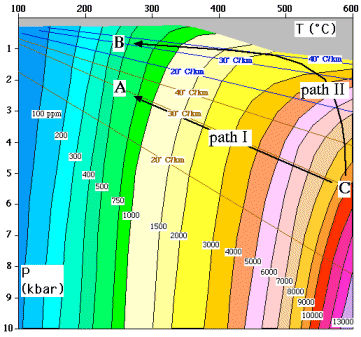The solubility of silica is about 500 ppm in pure water that is at a lithostatic pressure of about 200 Mpa at about 250°C (consistent with a depth between 5 and 10 km and a geothermal gradient in the order of 30°C/km, point A in Fig. 29). Dropping the fluid pressure to hydrostatic pressure (point B) reduces the solubility to about 400 ppm. The drop in pressure thus causes about 20% of dissolved quartz to precipitate and 10,000 kg of water is needed for every kg of vein quartz. The pressure sensitivity is even smaller at lower temperature. The large amount of fluid needed (fluid/rock ratio about 10,000 and at least 1000) is a problem. One source for the fluid can be metamorphic dewatering at deeper levels. Another possibility is recycling of water by pumping fluid in and out of the rock ("seismic pumping", Sibson et al. 1975) or convective flow, that allows the fluid multiple passes through the same veins (Etheridge et al. 1983; 1984). 
 

Figure 29. Contours of silica solubility (in ppm) in pure water as a function of pressure (P in kbar) and temperature (T in °C). Solubility is strongly temperature dependent, with a strong pressure dependency only in the low P and high T domain. PT-lines are drawn for geothermal gradients of 20, 30 and 40°C for a lithostatic pressure-depth gradient (brown, r=2.75·103 kg/m3) and a hydrostatic pressure-depth gradient (blue, r=1.0·103 kg/m3). Contours are based on the equation for silica solubility as a function of temperature and specific volume of pure water (Fournier & Potter 1982). Specific volume values are from tabulated data in Bowers (1995) (<2 kbar) or calculated with equations provided by Kerrick & Jacobs (1981) (>2 kbar). Reduction of fluid pressure (Pf) from lithostatic (point A) to hydrostatic (point B) leads to about 100 ppm (~20%) reduction in solubility at 250 °C and a geothermal gradient of 30 °C/km. Hot metamorphic fluid (point C) has a dramatically higher solubility (~10,000 ppm). Most silica would precipitate close to the source during slow ascent (path I) (Connolly 1997). Rapid mobile hydrofracture ascent (path II) would see silica precipitation much higher in the crust.

Metamorphic dewatering produces hot water at depth. Solubility of silica at source conditions of the fluid are high, in the order of >10,000 ppm (point C in Fig. 29). Cooling of the fluid as it flows upwards causes almost all of the dissolved quartz to precipitate at deep levels (Connolly 1997). One would thus expect most quartz veins to form just above the level of dewatering. However, extensive quartz veining is usually found at much shallower levels. It seems that metamorphic dewatering and normal advective (Darcian) upward flow of fluid cannot explain the formation of extensive vein sets at shallow levels: more than 90% of the dissolved quartz would have precipitated before reaching the veining level as flow is too slow to maintain any significant elevated fluid temperature. 

Metamorphic dewatering can, however, produce extensive quartz veining at or just above the brittle-ductile transition, without significant quartz precipitation at deeper levels, if the fluid can rise fast enough not too cool (much) before reaching the brittle-ductile transition. Mobile hydrofracturing provides the mechanism for such a rapid rise (Appendix A). The rise of water filled fractures at rates in the order of metres per second allows the water to stay hot until arrest in brittle levels of the crust (Bons in press b). Upon arrest (point A & B in Fig. 29), the water then still contains several thousands ppm of silica, which is immediately dumped as the water cools to the much lower ambient temperature. As is explained in Appendix A, arrest occurs in the base of the brittle region, where the fluid can enter pre-existing fractures or where a low (hydrostatic) fluid pressure causes leakage of the fluid into the wall rock. In the latter case, one can expect significant wall rock alteration to occur. 

Shear zones on small scales to crustal scales focus fluid flow, due to their enhanced permeability, either on the microscopic scale (dilatant grain boundaries or microfractures) or the macroscopic scale (fractures) (Connolly 1997, Thompson 1997). Many shear zones show evidence of enhanced fluid flow in the form of retrograde mineral reactions that involve hydration and/or the presence of veins (Rutter & Brodie 1985, Dipple & Ferry 1992, O'Hara & Haak 1992). Shear zones are also the preferred pathways for mobile hydrofractures, as they provide a relatively weak zone for hydrofracture propagation and, in case of crustal scale shear zones, provide a continuous pathway through the crust for ascending fluids. Many extensive vein systems are therefore associated with major fault and shear zone systems (Eisenlohr et al. 1989).

Veined fractures are usually regarded as the product of fluid flow. Hence, their study can provide insight in how fluid flows. This view should be reconsidered: veins that form from mobile hydrofracture arrest may tell us more about how fluid failed to flow. This philosophical point can perhaps best be explained with the analogy with granites: the shape and structures of granite bodies tell us most about the emplacement mechanism (stoping, ballooning, etc.) and much less about the mode of transport of granite melt (Clemens 1998). 

Significant supersaturation, open fluid-filled fracture space and repeated fracturing are characteristic for both veins that form from extensive flow through fracture networks and by arrest of mobile hydrofractures. Elongate blocky textures and evidence for crack sealing can be expected. Significant supersaturation can cause ongoing nucleation of precipitating minerals, which produces a blocky texture.