In this section we briefly define terms such as elasticity, viscosity and plasticity so that our use of these terms later in the discussion is clear.

All rocks show an elastic response to an imposed stress or strain rate. This means that there is a reversible, instantaneous deformation once the stress or strain rate is applied. Commonly the stress-strain relationship is linear although non-linear response is observed at low confining pressures and strains. Non-linear elastic constitutive relationships have been appealed to recently in some folding studies (see Hunt et al., 1996a,b), the response being the development of localised fold packets rather than a sinusoidal waveform with the Biot wavelength. We explore these effects further in Section 5.

It is common in geological arguments to specifically neglect elasticity under the pretext that the folding process is slow and is therefore intrinsically controlled by viscous behaviour, the elastic deformation being small compared to the viscous part of the total deformation. This is true so long as the deformation remains homogeneous throughout with no development of instabilities such as folds or shear bands.

A useful concept here is that of the Deborah Number, D_e. This is defined as

De =

(4)

Thus, for instance, if the process of interest is folding of an elastoviscous layer embedded in an elastoviscous material, the time scale for this process is the inverse of the amplification coefficient, , in expression (3). The relaxation time for Maxwell viscoelastic response is where is the viscosity and is the elastic shear modulus (see Jaeger, 1969, p. 102).

The common geological argument that elasticity can be neglected is an assertion that the Deborah Number is less than one. This is equivalent to saying that the relaxation time scales are always large in comparison to the time scales for the growth of instabilities in the deformation with the resulting corollary that geological deformations must always be homogeneous; this quite clearly is not true.

Instabilities such as folds and shear zones grow and evolve at their own separate time scales and the mere fact that they are ubiquitous in deformed rocks means that the time scales for the growth of these instabilities exceed the relaxation time scales for the material; that is D_e is greater than one for many geological processes. Neglect of instantaneous aspects of material behaviour such as elasticity and most types of plasticity, where the constitutive behaviour is rate insensitive, is admissible only if D_e << 1.

As indicated above, elastic behaviour is reversible; on the other hand there are essentially two types of constitutive behaviour that describe irreversible, permanent deformational response to imposed stress or strain rate boundary conditions.

One of these modes of behaviour is typically rate insensitive but commonly strongly pressure sensitive. The rate insensitivity implies that the physical and chemical processes operating during deformation are not influenced strongly by changes in temperature whilst the strong pressure sensitivity implies that these processes have a strong normal stress dependence, that is, they have a frictional character. Thus, the commonly accepted mechanism of deformation for these materials is fracturing and sliding on these fractures. Such processes can operate at all scales from the micro- or grain-scale, where the structures involved are microcracks or grain boundaries, to the regional scale where the structures involved are joints, fault systems and bedding planes.

The style of deformation described above is called plasticity and commonly the constitutive behaviour is described using a Mohr-Coulomb Yield Criterion with an associated or non-associated flow rule. We do not explore materials characterised by plastic behaviour in this paper. Examples of the folding of plastic materials can be found in Chapple (1969) and in Zhang et al. (1996). It appears that strain localisation behaviour of plastic materials strongly affects the buckling development of a plastic layer, resulting in more localised buckling growth in comparison with elastic or viscous materials.

The second of these irreversible modes of deformation is just the opposite to plasticity: the mechanical behaviour is strongly rate sensitive but pressure insensitive. This implies that the mechanisms of deformation are strongly temperature dependent but not dependent on changes in normal stress. The commonly accepted mechanisms of deformation for these materials are grain-scale crystal defect processes with or without atomic diffusion.

This style of deformation is called viscosity and commonly the constitutive behaviour is described in terms of a power-law dependence of the viscosity upon the strain rate. The constitutive relationship is

(5)

where are the components of the deviatoric stress tensor, are the components of the stretching and is the viscosity, given by

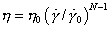(6)

where and 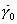are the reference viscosity and strain rate, and 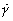is the equivalent strain rate. N is a constant which for many geological materials has values in the range 0.3 to 1. If N=1 the constitutive behaviour is called Newtonian Viscosity. The constitutive behaviour described by (5) is a coaxial constitutive law in that the principal axes of stress are always coaxial with the principal axes of the deformation rate.

Almost all of the literature on folding is concerned with linearly elastic materials, or Newtonian viscous materials or combinations of one of these materials embedded in the other. The results of studies of these materials predicts the operation of a Biot type wavelength selection process with the ultimate exponential amplification of a single dominant wavelength independent of the geometry of initial irregularities in the layer. Thus the resultant geometry is always periodic with one wavelength.

A much more interesting constitutive behaviour is the simple Maxwell elastoviscous material (see Jaeger, 1969, p. 102). This consists of a linear elastic element in series with a Newtonian viscous element. We are just starting to understand the complexity in behaviour that such Maxwell materials can exhibit during single layer folding. We explore some of this complexity in Section 4.