Fold Growth In Elastoviscous Materials
A study of fold growth in elastoviscous materials is particularly instructive since the range of possible behaviours is exceedingly rich. In part this is because there exist three time scales: the relaxation times of the single layer material and the embedding material respectively and the time scale associated with the fold evolution. If the time scale of the fold evolution is much slower than both relaxation times then the system behaves approximately like a viscous layer embedded in a viscous matrix. If, on the other hand, the fold evolution is much faster than both relaxation times then elastic in elastic behaviour ensues and so on.
This leads to a strong dependence of folding behaviour on strain rate. In what follows we concentrate on the simple Maxwell elastoviscous material.
As indicated in Section 2 the Maxwell elastoviscous material consists of a linear elastic element in series with a viscous material (see Jaeger, 1969, p. 102). The relaxation time, 
, for such a material is 
where 
is the viscosity of the viscous element and 
is the shear modulus for the elastic element.
If 
is the amplification factor from (3), then Mühlhaus et al. (1998) show that it is convenient to define a dimensionless quantity,
as 
= 
. Then, the behaviour of single layer Maxwell systems can be rationalised by examining various regimes for 
where
 |
(7) |
The function 
is plotted in Figure 9.
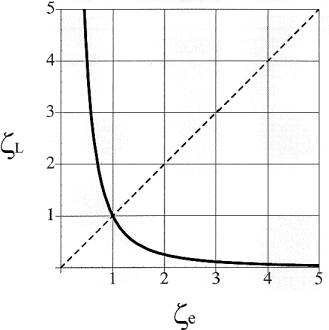
Figure 9: Domains of qualitatively different behaviour in dependency of the relaxation times 
of the plate material and 
of the supporting material. Spontaneous buckling instability occurs if 
leading to the generation of two "dominant" wavelengths. 
is shown as a solid line; 
is shown as a dashed line.
If 
³
0 only one dominant wavelength develops. Examples of the dispersion function are given in Figure 10(a) and Figure 10(b). However, if 
<0 two dominant wavelengths develop; the dispersion function is shown for 
, 
in Figure 10(c). These results are based on a linear stability analysis and some results of the growth of buckling instabilities within the various regimes of Figure 9 are given in Figure 11.
It is the development of two dominant wavelengths for the buckling of Maxwell materials that is perhaps the origin of parasitic folds in natural fold systems. Such behaviour is not possible in linear elastic or Newtonian viscous materials although such behaviour is perhaps possible in other non linear rheologies which have not yet been explored. Notice however that fold systems such as those shown in Figure 11 are still quite regular in that they result from the superposition of two periodic wavetrains of two different wavelengths. There is still none of the irregularity demonstrated by natural folds (see Figure 2 and Figure 3).
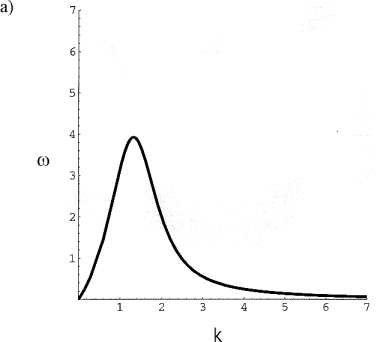
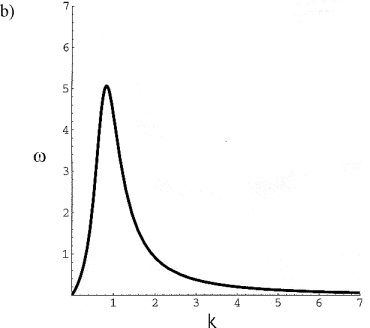
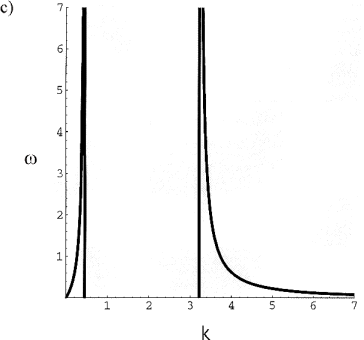
Figure 10: a) Dispersion function for D2=0, N=1.0, 
: 
and 
. b) Dispersion function for D2=0, N=1.0, : 
and 
. c) Dispersion function for relaxation time in the region for 
: 
and 
. Notice two wavenumbers are now amplified. The value of 1.0 for the wavenumber corresponds to the Biot wavelength given by expression (1).
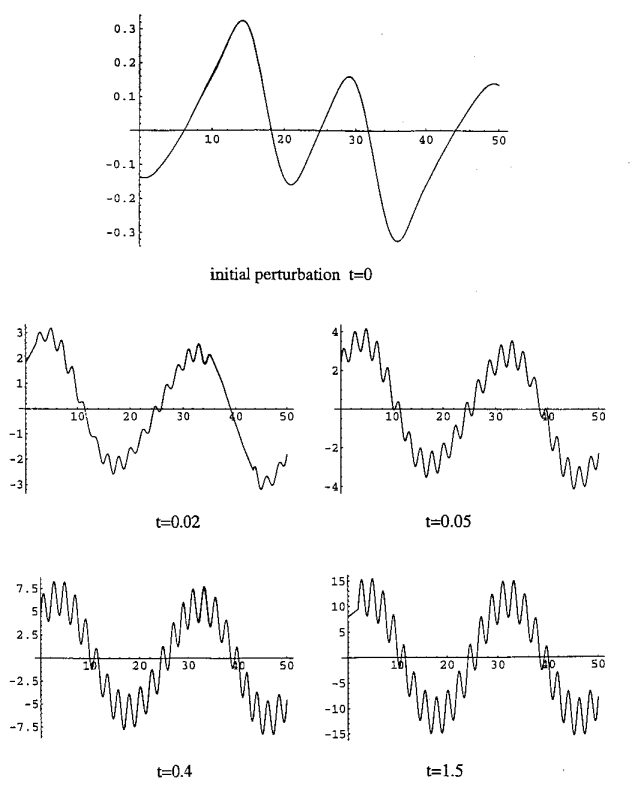
Figure 11: Numerical solutions for growth of fold system in the field 
in Figure 9; 
and 
. The indicated times are dimensionless and are fractions of the viscous, fold amplification, time constant.
However there is another extremely important aspect of the buckling of Maxwell materials; namely a strong dependence of fold amplification upon strain rate, viscosity, elastic moduli and competency contrast. Under some combinations of these four variables, the model shown in Figure 1 undergoes only homogeneous shortening with no wavelength selection processes operating and, hence, no buckling processes. This is the type of behaviour illustrated in Figure 6(b). Under other combinations, buckling is well developed as in the case of Figure 6(c). As has been alluded to earlier in this paper, whether the homogeneous shortening mode or the pure buckling mode dominates in a particular situation depends on the competition between the viscous relaxation rate and the buckling amplification rate and is expressed through the Deborah Number given in (4). The situation is treated and illustrated in the sequence of papers: Zhang et al. (1996), Mancktelow (1999), Zhang et al. (1999 a,b,c), and Zhang et al. (2000).
One important aspect of this behaviour is that initial geometrical perturbations are preserved and amplified in an entirely passive manner or a manner characterized by initial passive amplification (limb dips reach higher angles) plus later dynamic growth at one end of the spectrum of behaviour, where homogeneous shortening plays a critical role. Such initial geometrical perturbations tend to be obliterated at the other end of the spectrum of behaviour where wavelength selection processes operate and one or more wavelengths become dynamically amplified. For buckling at this end of the spectrum, the mechanical ability of the system to be able to select new wavelengths related to competency contrast and layer thickness is critical. This means that with such an ability, a weak layer (small competency contrast) would not support the growth of initial broad geometrical perturbations (initial wavelength too large), and similarly a strong layer (large competency contrast) would not support the growth of initial very small perturbations (initial wavelengths too small). These aspects are illustrated in Figure 6 but also in Figure 12 to Figure 14.
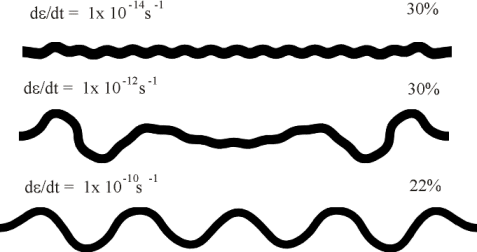
Figure 12: Enhancement of dynamic fold growth by increasing strain rate (d
e/dt). Competency contrast (R) is 200 in all three models. Corresponding material properties are: hL = 2x1021 Pa s, he = 1x1019 Pa s, EL = 7x1011 Pa, Ee = 3.5x109 Pa, mL = 2.8x1011 Pa and me = 1.4x109 Pa. Note that in the model with de/dt = 1x 10-14 s-1, the dynamic fold growth rate is very small so that homogeneous straining is dominating at the 30% bulk shortening stage.
Figure 13: Enhancement of dynamic fold growth with increasing competency contrast (R) between the layer and the medium at a particular strain rate (d
e/dt = 1x10-14 s-1 for all the models). Material properties for the model with R = 20 are: hL = 2x1023 Pa s, he = 1x1022 Pa s, EL = 3.5x1010 Pa, Ee = 1.75x109 Pa, mL = 1.4x1010 Pa and me = 0.7x109 Pa. For the other models parameters for the medium (he, Ee and me) are decreased to form the indicated R values.
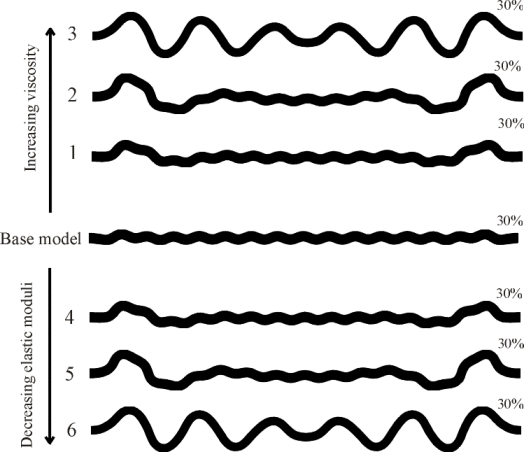
Figure 14: Enhancement of dynamic fold growth with increasing viscosity or with decreasing elastic moduli at a particular strain rate and competency contrast (d
e/dt = 1x10-14 s-1 and R = 100 for all the models). Material properties for base model are: hL = 1x1021 Pa s, he = 1x1019 Pa s, EL = 3.5x1011 Pa, Ee = 3.5x109 Pa, mL = 1.4x1011 Pa and me = 1.4x109 Pa. Viscosity (hL and he) are increased by 10, 100 and 1000 times in model 1, 2 and 3, with respect to the base model. Elastic moduli (EL, Ee, mL and me) are decreased by 10, 100 and 1000 times in model 4, 5 and 6, with respect to the base model. Note that the base model is dominated by homogeneous shortening and passive amplification of initial geometrical perturbations, similar to the results of one of Macktelow’s (1999) finite element models.The essential processes operating here are:
(i) Increasing strain rate has the effect of decreasing the importance of homogeneous straining and enhancing dynamic amplification. This is demonstrated in Figure 12 which shows the results of a series of numerical experiments at 10-14 s-1, 10-12 s-1 and 10-10 s-1 strain rate. For the identical initial geometry and material properties, buckling behaviour varies from the domination of homogeneous shortening and passive amplification of initial geometrical perturbations at a strain rate of 10-14 s-1 (this is similar to the results of Mancktelow, 1999) to the domination of dynamic folding at 10-10 s-1.
(ii) Increasing the competency contrast (R) at a particular strain rate increases the tendency towards dynamic fold amplification as shown in Figure 13. Note that the model with a small competency contrast (R=20) displays a more irregular fold train due to relatively weak dynamic fold growth and this seems to be closer to fold geometries observed in Nature.
(iii) Decreasing the absolute value of the elastic moduli for the folding layer increases the tendency towards dynamic amplification as shown Figure 14 (bottom part).
(iv) Increasing the absolute value of the viscosity for the folding layer increases the tendency towards dynamic amplification as shown Figure 14 (top part). This can have an identical effect on folding as decreasing the value of the elastic moduli.